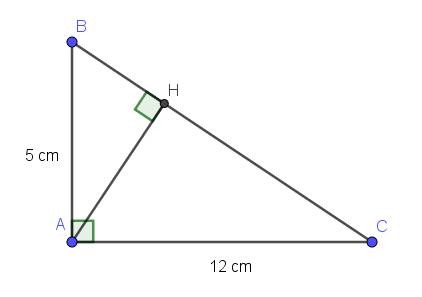
cho tam giác abc vuông tại a, đường cao ah (h thuộc bc) biết ab=5, ac=12 hảy tính độ dài các cạch bh,ch,ah
Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông
ΔABC vuông tại A
=>AB^2+AC^2=BC^2
=>BC^2=5^2+12^2=169
=>BC=13
Xét ΔABC vuông tại A có AH là đường cao
nên AH*BC=AB*AC; AB^2=BH*BC; AC^2=CH*CB
=>AH=5*12/13=60/13; BH=5^2/13=25/13; CH=12^2/13=144/13
Đúng 0
Bình luận (0)
Lời giải:
Áp dụng hệ thức lượng trong tam giác vuông ta có:
$\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{5^2}+\frac{1}{12^2}=\frac{169}{3600}$
$\Rightarrow AH=\frac{60}{13}$ (cm)
Áp dụng định lý Pitago:
$BH=\sqrt{AB^2-AH^2}=\sqrt{5^2-(\frac{60}{13})^2}=\frac{25}{13}$ (cm)
$CH=\sqrt{AC^2-AH^2}=\sqrt{12^2-(\frac{60}{13})^2}=\frac{144}{13}$ (cm)
Đúng 0
Bình luận (0)
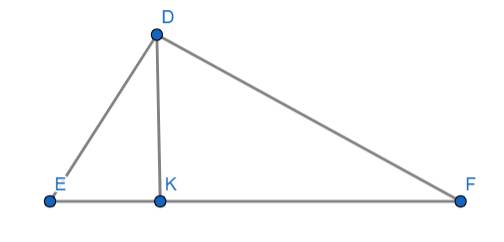
Cho Tam giác DEF biết EF bằng 7,5cm DF bằng 4,5cm DE bằng 6cm a) Tính đường cao DK của tam giác DEF b) Tính EK và FK
Xét ta có:
\(EF^2=7,5^2=56,25\left(cm\right)\) (1)
Mà: \(DF^2+DE^2=4,5^2+6^2=56,25\left(cm\right)\) (2)
Từ (1) và (2) ta có:
\(EF^2=DE^2+DF^2\)
\(\Rightarrow\Delta DEF\) vuông tại D có đường cao DK
a) Áp dụng hệ thức hai cạnh góc vuông và đường cao ta có:
\(\dfrac{1}{DK^2}=\dfrac{1}{DE^2}+\dfrac{1}{DF^2}\)
\(\Rightarrow DK^2=\dfrac{DE^2DF^2}{DF^2+DF^2}\Rightarrow DK=\sqrt{\dfrac{DE^2DF^2}{DF^2+DE^2}}\)
\(\Rightarrow DK=\sqrt{\dfrac{4,5^2\cdot6^2}{4,5^2+6^2}}=3,6\left(cm\right)\)
b) Áp dụng hệ thức hình chiếu và cạnh góc vuông ta có:
\(\left\{{}\begin{matrix}DE^2=EF\cdot EK\\DF=EF\cdot FK\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}EK=\dfrac{DE^2}{EF}\\FK=\dfrac{DF^2}{EF}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}EK=\dfrac{6^2}{7,5}=4,8\left(cm\right)\\FK=\dfrac{4,5^2}{7,5}=2,7\left(cm\right)\end{matrix}\right.\)
Đúng 2
Bình luận (0)
a: Xét ΔDEF có EF^2=DE^2+DF^2
nên ΔDEF vuông tại D
Xét ΔDEF vuông tại D có DK là đường cao
nên DK*FE=DE*DF
=>DE*7,5=27
=>DE=3,6cm
b: ΔDEF vuông tại D có DK là đường cao
nên EK*EF=ED^2
=>EK=6^2/7,5=4,8cm
FK=7,5-4,8=2,7cm
Đúng 0
Bình luận (2)
Cho hình thang vuông ABCD. Góc A=góc D (=90 độ). Biết AB=9cm; CD=16cm; BC=25cm. Trên BC lấy E sao cho BE=BA. Tính:
a) Góc AED
b) Diện tích ABCD; diện tích tam giác AED
Bài 3:Cho tam giác ABC vuông tại A.Có AH là đường cao từ H kẻ HM,HN vuông góc với AB,AC. CM : AM.AB=AN.AC Giúp mik với ạ(chi tiết)
ΔAHB vuông tại H có HM là đường cao
nên AM*AB=AH^2
ΔAHC vuông tại H có HN là đường cao
nên AN*AC=AH^2
=>AM*AB=AN*AC
Đúng 0
Bình luận (0)
Bài 2: cho tam giác ABC vuông tại A.Có AH là đường cao.Tính BH,biết AH=2cm;BC=5cm.
Bài 3:Cho tam giác ABC vuông tại A.Có AH là đường cao từ H kẻ HM,HN vuông góc với AB,AC. CM : AM.AB=AN.AC Giúp mik với ạ chiều cần gấp lắm(chi tiết giúp mik a)
3:
ΔAHB vuông tại H có HM là đường cao
nên AM*AB=AH^2
ΔAHC vuông tại H có HN là đường cao
nên AN*AC=AH^2
=>AM*AB=AN*AC
Đúng 0
Bình luận (0)
Cho tam giác ABC Vuông tại A Có AB=3cm , AC=4cm , AH là đường cao , AD là phân giác Tính BC,BH,CH,BD,CD,HD. Giúp mik với ạ
Lời giải:
Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5$ (cm)
Áp dụng hệ thức lượng trong tam giác vuông:
$BH=\frac{AB^2}{BC}=\frac{3^2}{5}=\frac{9}{5}=1,8$ (cm)
$CH=BC-BH=5-1,8=3,2$ (cm)
$\frac{BD}{CD}=\frac{AB}{AC}=\frac{3}{4}$
$\Rightarrow \frac{BD}{BD+CD}=\frac{3}{7}$
Hay $\frac{BD}{BC}=\frac{3}{7}\Rightarrow BD=\frac{3}{7}.BC=\frac{3}{7}.5=\frac{15}{7}$ (cm)
$CD=BC-BD=5-\frac{15}{7}=\frac{20}{7}$ (cm)
$HD=BD-BH=\frac{15}{7}-1,8=\frac{12}{35}$ (cm)
Đúng 2
Bình luận (3)
Cho tam giác ABC Voòng tại A Có AB=3cm ÁC=4cm AH là đường cao AD là phân giác Tính BC,BH,CH,BD,CD,HD
ΔABC vuông tại A
=>AB^2+AC^2=BC^2
=>BC=căn 3^2+4^2=5cm
ΔABC vuông tại A có AH là đường cao
nên AH*BC=AB*AC; BH*BC=BA^2; CH*CB=CA^2
=>AH=3*4/5=2,4cm; BH=3^2/5=1,8cm; CH=4^2/5=3,2cm
ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/3=CD/4=(BD+CD)/(3+4)=5/7
=>BD=15/7cm; CD=20/7cm
Đúng 0
Bình luận (0)
Cho tam giác ABC vioong tại A biết AB=3cm , AC=4cm Tính tam giác ABC
Xét ΔABC vuông tại A áp dụng định lý Py-ta-go ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC^2=3^2+4^2\)
\(\Rightarrow BC^2=9+16\)
\(\Rightarrow BC^2=25\)
\(\Rightarrow BC=\sqrt{25}\)
\(\Rightarrow BC=5\left(cm\right)\)
Đúng 0
Bình luận (0)
cho tam giác MNP vuông tại M có MK đường cao.biết MP = 10 cm, KP = 8 cm .Tính MK, NK, MN
Xem chi tiết
Áp dụng hệ thức trong tam giác vuông có:
\(MP^2=PK.PN\Leftrightarrow PN=12,5\left(cm\right)\)
\(MN=\sqrt{PN^2-MP^2}=7,5cm\)
\(MN^2=NK.NP\Leftrightarrow NK=4,5\left(cm\right)\)
\(MK^2=KN.KP=4,5.8=36\Leftrightarrow MK=6\left(cm\right)\)
Vậy...
Đúng 1
Bình luận (0)
NP=MP^2/PN=10^2/8=12,5cm
MK=căn 10^2-8^2=6cm
NK=6^2/8=4,5cm
MN=căn 12,5^2-10^2=7,5cm
Đúng 0
Bình luận (0)
`@`Phamdanhv.
ảnh mình không tải được , bạn vào link này nhé
`=>`
blob:https://www.facebook.com/87ade4e1-6c0b-45ee-b42f-df163ba3224e
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có đường cao là ah HP = 9 cm HC = 16 cm
a)tính AB AC ah
b)Gọi D và E lần lượt là hình chiếu vuông góc của h trên AB và AC. tứ giác AD he là hình gì
a: BC=BH+CH=25cm
Xét ΔABC vuông tại A có AH là đường cao
nên AB^2=BH*BC; AC^2=CH*BC; AH^2=HB*HC
\(AB=\sqrt{BH\cdot BC}=\sqrt{9\cdot25}=15\left(cm\right)\)
\(AC=\sqrt{16\cdot25}=20\left(cm\right)\)
\(AH=\sqrt{HB\cdot HC}=12\left(cm\right)\)
b: Xét tứ giác ADHE có
góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật
Đúng 0
Bình luận (0)