Question

cho tam giác abc vuông tại a, đường cao ah (h thuộc bc) biết ab=5, ac=12 hảy tính độ dài các cạch bh,ch,ah  

Answer 1

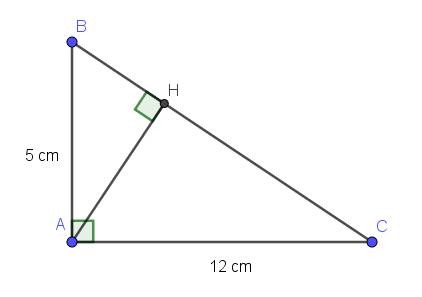
ΔABC vuông tại A

=>AB^2+AC^2=BC^2

=>BC^2=5^2+12^2=169

=>BC=13

Xét ΔABC vuông tại A có AH là đường cao

nên AH*BC=AB*AC; AB^2=BH*BC; AC^2=CH*CB

=>AH=5*12/13=60/13; BH=5^2/13=25/13; CH=12^2/13=144/13

Answer 2

Lời giải:
Áp dụng hệ thức lượng trong tam giác vuông ta có:
$\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{5^2}+\frac{1}{12^2}=\frac{169}{3600}$

$\Rightarrow AH=\frac{60}{13}$ (cm) 

Áp dụng định lý Pitago:

$BH=\sqrt{AB^2-AH^2}=\sqrt{5^2-(\frac{60}{13})^2}=\frac{25}{13}$ (cm) 

$CH=\sqrt{AC^2-AH^2}=\sqrt{12^2-(\frac{60}{13})^2}=\frac{144}{13}$ (cm) 

Answer 3

Hình vẽ: