Ôn tập Hệ thức lượng trong tam giác vuông

TÓM TẮT KIẾN THỨC CẦN NHỚ

1. Các hệ thức về cạnh và đường cao trong tam giác vuông

Cho tam giác \(ABC\), vuông tại \(A\). Đường cao \(AH\). Độ dài các đoạn thẳng được kí hiệu như hình vẽ. Khi đó ta có:

• \(b^2=ab'\); \(c^2=ac'\).
• \(h^2=b'.c'\)
• \(ah=bc\)
• \(\dfrac{1}{h^2}=\dfrac{1}{b^2}+\dfrac{1}{c^2}\)

2. Định nghĩa các tỉ số lượng giác của góc nhọn

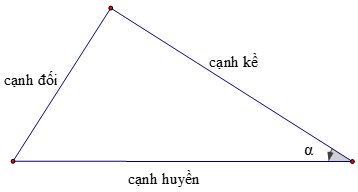
• \(\sin \alpha =\dfrac{\text{cạnh đối}}{\text{cạnh huyền}}\);
• \(\cos \alpha =\dfrac{\text{cạnh kề}}{\text{cạnh huyền}}\);
• \(\tan \alpha =\dfrac{\text{cạnh đối}}{\text{cạnh kề}}\);
• \(\cot \alpha =\dfrac{\text{cạnh kề}}{\text{cạnh đối}}\).

3. Một số tính chất của các tỉ số lượng giác

a) Cho \(\alpha,\beta\) là hai góc phụ nhau. Khi đó ta có:

• \(\sin\alpha=\cos\beta\); \(\cos\alpha=\sin\beta\)
• \(\tan\alpha=\cot\beta\); \(\cot\alpha=\tan\beta\)

b) Cho góc nhọn \(\alpha\), ta có:

• \(0< \sin\alpha< 1;0< \cos\alpha< 1\);
• \(\tan\alpha>0;\cot\alpha>0\);
• \(\sin^2\alpha+\cos^2\alpha=1\);
• \(\tan\alpha=\dfrac{\sin\alpha}{\cos\alpha};\cot\alpha=\dfrac{\cos\alpha}{\sin\alpha}\);
• \(\tan\alpha.\cot\alpha=1\).

3. Các hệ thức về cạnh và góc trong tam giác vuông

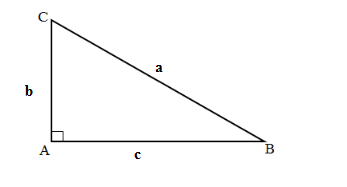
• \(b=a.\sin B;c=a.\sin C\)
• \(b=a.\cos C;c=a.\cos B\)
• \(b=c.\tan B;c=b.\tan C\)
• \(b=c.\cot C;c=b.\cot B\)