\(y=x+1-\dfrac{4}{x+2}\left(đk:x\ne-2\right)\)
\(y'=1+\dfrac{4}{\left(x+2\right)^2}>0\forall x\ne-2\)
\(\Rightarrow\) Hàm số y đồng biến trên \(R|\left\{-2\right\}\)
1)GTNN của hs y=x2+5/x-3 trên đoạn [3;6]
2)GTLN của hs y=sinx+căn3.cosx trên đoạn [0;bi]
3) Đk của m để pt x+căn1-x =m có nghiệm
Mn giúp mk vs ạ mk cảm ơn
Tìm GTLN - GTNN của:
1)
Cho hàm số y = x 2 - 2 | x | + 2 và các mệnh đề
(1) Hàm số trên liên tục trên R
(2) Hàm số trên có đạo hàm tại x = 0
(3) Hàm số trên đạt GTNN tại x = 0.
(4) Hàm số trên đạt GTLN tại x = 0.
(5) Hàm số trên là hàm chẵn
(6) Hàm số trên cắt trục hoành tại duy nhất một điểm
Trong các mệnh đề trên, số mệnh đề đúng là
A. 1
B. 2
C. 3
D. 4
1. Tìm m sao cho \(y=\frac{m\sin x+4}{\sin x+m}\)nghịch biến trên \(\left(0,\frac{\eta}{2}\right)\)
2. Tìm m sao cho \(y=\frac{\cos x+1}{m\cos x+2}\)nghịch biến trên \(\left(0,\frac{\eta}{2}\right)\)
Với giá trị nào của x thì đồ thị hàm số y = 2 / 3 x nằm phía trên đường thẳng y = 1?
A. x > 0 B. x < 0
C. x = 0 D. x < 1
Cho hàm số y = x 3 - 2 x 2 - 1 (1) và các mệnh đề
(1) Điểm cực trị của hàm số (1) là x = 0 hoặc x = 4/3
(2) Điểm cực trị của hàm số (1) là x = 0 và x = 4/3
(3) Điểm cực trị của đồ thị hàm số (1) là x = 0 và x = 4/3
(4) Cực trị của hàm số (1) là x = 0 và x = 4/3
Trong các mệnh đề trên, số mệnh đề sai là:
A. 0
B. 1
C. 2
D. 3
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$
Xét các mệnh đề sau
(1) log2(x - 1)2 + 2log2(x+1) = 6
<=> 2log2(x-1) + 2log2(x+1) = 6
(2) log2(x2+1) ≥ 1 + log2|x|; ∀ x ∈ R
(3) xlny = ylnx; ∀ x > y > 2
( 4 ) log 2 2 2 x - 4 log 2 x - 4 = 0 ⇔ log 2 2 x - 4 log 2 x - 3 = 0
Số mệnh đề đúng là
A. 0
B. 1
C. 2
D. 3
Trong không gian Oxyz cho mặt cầu ( S ) : ( x - 1 ) 2 + ( y + 2 ) 2 + ( z - 2 ) 2 = 4 và mặt phẳng (P): x-y+2z-1=0 Gọi M là một điểm bất kì trên mặt cầu (S) Khoảng cách từ M đến (P) có giá trị nhỏ nhất bằng
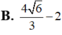
