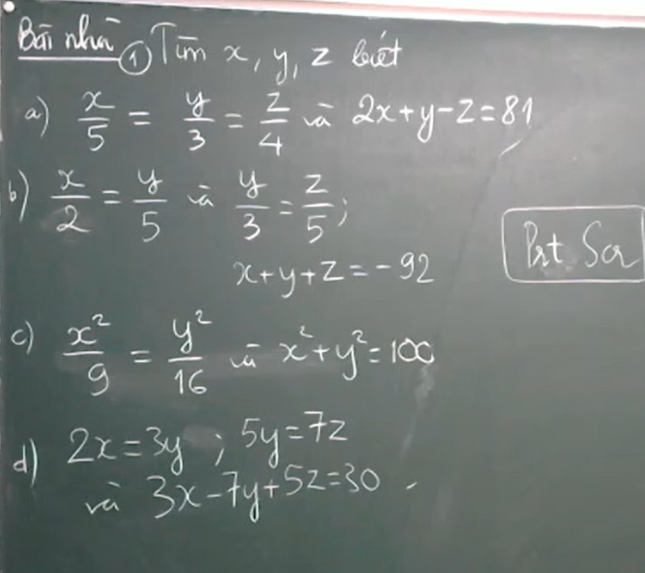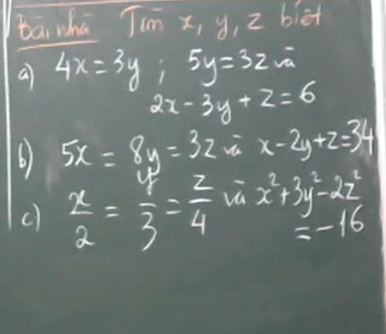Bài 5:
a: Xét ΔOAC vuông tại A và ΔOBD vuông tại B có
OA=OB
\(\hat{AOC}=\hat{BOD}\) (hai góc đối đỉnh)
Do đó: ΔOAC=ΔOBD
b: ΔOAC=ΔOBD
=>OC=OD và AC=BD
Xét ΔEOC vuông tại O và ΔEOD vuông tại O có
EO chung
OC=OD
Do đó: ΔEOC=ΔEOD
c: ΔEOC=ΔEOD
=>EC=ED
Ta có: EC=ED
ED=EB+BD
Do đó: EC=EB+BD
mà BD=AC
nen EC=EB+CA
Bài 4:
a: Xét ΔBHA và ΔBHE có
BH chung
HA=HE
BA=BE
Do đó: ΔBHA=ΔBHE
b: ΔBHA=ΔBHE
=>\(\hat{ABH}=\hat{EBH}\)
Xét ΔBAK và ΔBEK có
BA=BE
\(\hat{ABK}=\hat{EBK}\)
BK chung
Do đó: ΔBAK=ΔBEK
=>\(\hat{BKA}=\hat{EKB}\)
=>KB là phân giác của góc AKE
ΔBAK=ΔBEK
=>\(\hat{BAK}=\hat{BEK}\)
=>\(\hat{BEK}=90^0\)
c: Xét ΔHAI vuông tại H và ΔHEB vuông tại H có
HA=HE
HI=HB
Do đó: ΔHAI=ΔHEB
=>\(\hat{HAI}=\hat{HEB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AI//BE
mà EK⊥BE
nên EK⊥IA
Bài 3:
a: Xét ΔDBE và ΔDAK có
DB=DA
\(\hat{BDE}=\hat{ADK}\) (hai góc đối đỉnh)
DE=DK
Do đó: ΔDBE=ΔDAK
=>\(\hat{DBE}=\hat{DAK}\)
mà hai góc này là hai góc ở vị trí so le trong
nên BE//AK
=>BC//AK
b: ΔDBE=ΔDAK
=>BE=AK
mà BE=EC
nên EC=AK
Xét ΔAKE và ΔECA có
KA=EC
\(\hat{KAE}=\hat{CEA}\) (hai góc so le trong, AK//CE)
AE chung
Do đó: ΔAKE=ΔECA
c: ΔAKE=ΔECA
=>EK=AC
ΔKEA=ΔCAE
=>\(\hat{KEA}=\hat{CAE}\)
mà hai góc này là hai góc ở vị trí so le trong
nên KE//AC
Xét ΔIEK và ΔIAC có
IE=IA
\(\hat{IEK}=\hat{IAC}\)
EK=AC
Do đó: ΔIEK=ΔIAC
=>\(\hat{EIK}=\hat{AIC}\)
mà \(\hat{AIC}+\hat{EIC}=180^0\) (hai góc kề bù)
nên \(\hat{EIK}+\hat{EIC}=180^0\)
=>K,I,C thẳng hàng
mà IK=IC
nên I là trung điểm của KC
Bài 1. a) Vì AI là tia phân giác của góc BAC nên ảnh BAI = ảnh IAC. Lại có AD = AB (giả thiết) và AI chung. Xét hai tam giác ABI và ADI, chúng có hai cạnh AB = AD, AI chung và một cặp góc kèm giữa bằng nhau nên hai tam giác này bằng nhau theo trường hợp cạnh – góc – cạnh. Do đó suy ra BI = ID. b) Từ việc hai tam giác ABI và ADI bằng nhau suy ra ảnh ABI = ảnh IAD. Điểm E nằm trên cạnh AB nên ảnh EBI = ảnh ABI. Mặt khác ảnh IAD và ảnh IDC là hai góc cùng chắn cung IC trong tam giác IDC nên ảnh IAD = ảnh IDC. Suy ra ảnh EBI = ảnh IDC. c) Ta có BI = ID (phần a) và vừa chứng minh được ảnh EBI = ảnh IDC. Hai tam giác IBE và IDC còn có ảnh IEB và ảnh ICD là hai góc đối đỉnh. Do đó hai tam giác IBE và IDC bằng nhau theo trường hợp góc – cạnh – góc. Từ đây suy ra ảnh AIB = ảnh AID và EB = DC. Bài 2. a) Vì AB = AC và AM = AN nên MB = NC. Xét hai tam giác BNM và CNM: chúng có MB = NC, MN chung và ảnh BMN = ảnh NCM (hai góc đối đỉnh). Theo trường hợp cạnh – góc – cạnh suy ra hai tam giác bằng nhau, do đó BN = CM. b) Từ BN = CM và MB = NC (phần a) xét hai tam giác BMC và CNB: chúng có hai cặp cạnh bằng nhau và góc BMC = CNB (hai góc đối đỉnh) nên hai tam giác này bằng nhau. Tương tự, hai tam giác nhỏ BIM và CIN cũng bằng nhau, suy ra các đoạn và góc tương ứng bằng nhau.