a.
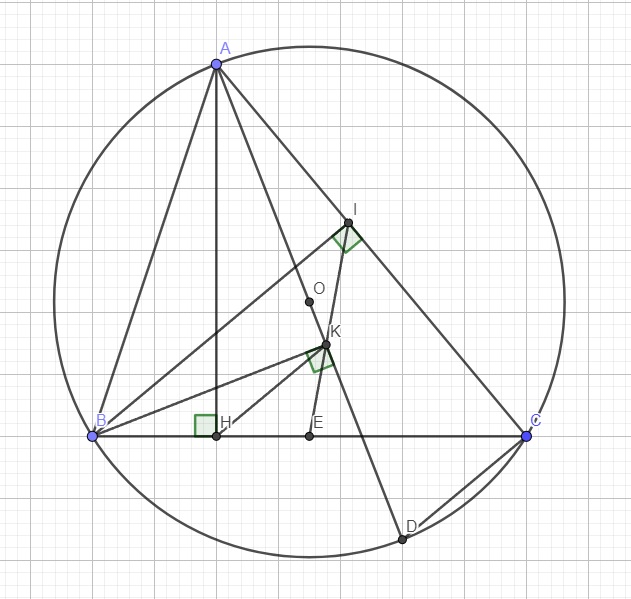
Theo giả thiết, do \(AH\perp BC;BK\perp AD;BI\perp AC\)
\(\Rightarrow\widehat{AHB}=\widehat{AKB}=\widehat{AIB}=90^0\)
\(\Rightarrow5\) điểm H, K, I, A, B cùng thuộc đường tròn đường kính AB
Nên tứ giác AIKH nội tiếp đường tròn đường kính AB
\(\Rightarrow\widehat{BIK}=\widehat{BAK}\) (cùng chắn AK)
Mà \(\widehat{BAK}=\widehat{BCD}\) (cùng chắn BD của (O))
\(\Rightarrow\widehat{BIK}=\widehat{BCD}\)
AD là đường kính của (O) \(\Rightarrow\widehat{ACD}=90^0\) (góc nt chắn nửa đường tròn)
\(\Rightarrow CD\perp AC\Rightarrow CD||BI\) (cùng vuông góc AC)
\(\Rightarrow\widehat{BCD}=\widehat{IBC}\) (so le trong)
\(\Rightarrow\widehat{BIK}=\widehat{IBC}\) (1)
Mà \(\widehat{IBC}=\widehat{CAH}\) (cùng phụ \(\widehat{ACB}\)) (2)
\(\widehat{CAH}+\widehat{IKH}=180^0\) (do AIKH nội tiếp) (3)
(1);(2);(3) \(\Rightarrow\widehat{BIK}+\widehat{IKH}=180^0\)
\(\Rightarrow HK||BI\) (hai góc trong cùng phía bù nhau)
\(\Rightarrow HK\perp AC\) (do \(BI\perp AC\))
c.
Gọi E là giao điểm của IK và BC
Từ (1): \(\widehat{BIK}=\widehat{IBC}\) \(\Rightarrow\Delta EBI\) cân tại E
\(\Rightarrow EB=EI\) (6)
Mặt khác \(BI\perp AC\Rightarrow\widehat{IBC}+\widehat{ECI}=90^0\)
\(\widehat{BIC}=90^0\Rightarrow\widehat{BIK}+\widehat{EIC}=90^0\)
\(\Rightarrow\widehat{ECI}=\widehat{EIC}\)
\(\Rightarrow\Delta EIC\) cân tại E
\(\Rightarrow EC=EI\) (7)
(6);(7) \(\Rightarrow EB=EC\)
Hay E là trung điểm của BC
Mà BC cố định nên E cố định
\(\Rightarrow\) Khi A di động trên cung lớn BC thì đường thẳng IK luôn đi qua điểm cố định là trung điểm của BC.
b.
Xét hai tam giác AHB và ACD có:
\(\left\{{}\begin{matrix}\widehat{AHB}=\widehat{ACD}=90^0\\\widehat{ABH}=\widehat{ADC}\left(\text{cùng chắn AC}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AHB\sim\Delta ACD\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{AD}=\dfrac{BH}{CD}\Rightarrow AB.CD=AD.BH\) (4)
Xét hai tam giác AHC và ABD có:
\(\left\{{}\begin{matrix}\widehat{AHC}=\widehat{ABD}=90^0\\\widehat{ACH}=\widehat{ADB}\left(\text{cùng chắn AB}\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AHC\sim\Delta ABD\left(g.g\right)\)
\(\Rightarrow\dfrac{AC}{AD}=\dfrac{CH}{BD}\Rightarrow AC.BD=AD.HC\) (5)
(4);(5) \(\Rightarrow AB.CD+AC.BD=AD.BH+AD.HC=AD\left(BH+HC\right)=AD.BC\)