Vẽ hình giúp mình với nhé cảm ơn nhiều ạ
6:
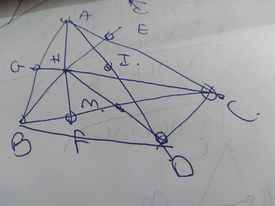
a: Xét tứ giác BHCD có
M là trung điểm chung của BC và HD
nên BHCD là hình bình hành
b: BHCD là hình bình hành
=>BH//CD và CH//BD
BH//CD
BH vuông góc AC
Do đó: CD vuông góc AC
=>ΔCAD vuông tại C
CH//BD
CH vuông góc AB
Do đó: BD vuông góc BA
=>ΔABD vuông tại B
c: Xét tứ giác ABDC có
\(\widehat{ABD}+\widehat{ACD}=90^0+90^0=180^0\)
=>ABDC là tứ giác nội tiếp đường tròn đường kính AD
=>ABDC nội tiếp (I)
=>IA=IB=IC=ID
Đúng 2
Bình luận (0)
Vẽ hình và giải chi tiết giúp mình với, đang cần gấp cảm ơn nhiều ạ
Vẽ hình và giải chi tiết giúp em với ạ Cảm ơn mọi người nhiều ạ
