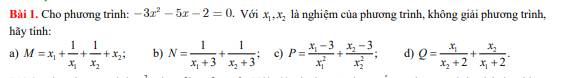Ta có: \(-3x^2-5x-2=0\)
Theo định lý vi-et ta có:
\(x_1+x_2=-\dfrac{b}{a}=-\dfrac{-5}{-3}=-\dfrac{5}{3}\)
\(x_1x_2=\dfrac{c}{a}=\dfrac{-2}{-3}=\dfrac{2}{3}\)
a) \(M=x_1+\dfrac{1}{x_1}+\dfrac{1}{x_2}+x_2\)
\(M=\left(x_1+x_2\right)+\dfrac{x_1+x_2}{x_1x_2}\)
\(M=-\dfrac{5}{3}+\dfrac{-\dfrac{5}{3}}{\dfrac{2}{3}}=-\dfrac{25}{6}\)
b) \(N=\dfrac{1}{x_1+3}+\dfrac{1}{x_2+3}\)
\(N=\dfrac{x_2+3+x_1+3}{\left(x_1+3\right)\left(x_2+3\right)}\)
\(N=\dfrac{\left(x_1+x_2\right)+6}{x_1x_2+3\left(x_1+x_2\right)+9}\)
\(N=\dfrac{-\dfrac{5}{3}+6}{\dfrac{2}{3}+3\cdot-\dfrac{5}{3}+9}=\dfrac{13}{14}\)
c) \(P=\dfrac{x_1-3}{x^2_1}+\dfrac{x_2-3}{x^2_2}\)
\(P=\dfrac{x^2_2\left(x_1-3\right)+x^2_1\left(x_2-3\right)}{x^2_1x^2_2}\)
\(P=\dfrac{x^2_2x_1+x^2_1x_2-3x^2_2-3x^2_1}{\left(x_1x_2\right)^2}\)
\(P=\dfrac{x_1x_2\left(x_1+x_2\right)-3\left[\left(x_1+x_2\right)^2-2x_1x_2\right]}{\left(x_1x_2\right)^2}\)
\(P=\dfrac{\dfrac{2}{3}\cdot-\dfrac{5}{3}-3\cdot\left[\left(-\dfrac{5}{3}\right)^2-2\cdot\dfrac{2}{3}\right]}{\left(\dfrac{2}{3}\right)^2}=-\dfrac{49}{4}\)
d) \(Q=\dfrac{x_1}{x_2+2}+\dfrac{x_2}{x_1+2}\)
\(Q=\dfrac{x_1\left(x_1+2\right)+x_2\left(x_2+2\right)}{\left(x_2+2\right)\left(x_1+2\right)}\)
\(Q=\dfrac{x^2_1+2x_1+x_2^2+2x_2}{x_1x_2+2x_2+2x_1+4}\)
\(Q=\dfrac{\left(x^2_1+x^2_2\right)+2\left(x_1+x_2\right)}{x_1x_2+2\left(x_1+x_2\right)+4}\)
\(Q=\dfrac{\left(x_1+x_2\right)^2-2x_1x_2+2\left(x_1+x_2\right)}{x_1x_2+2\left(x_1+x_2\right)+4}\)
\(Q=\dfrac{\left(-\dfrac{5}{3}\right)^2-2\cdot\dfrac{2}{3}+2\cdot-\dfrac{5}{3}}{\dfrac{2}{3}+2\cdot-\dfrac{5}{3}+4}=-\dfrac{17}{12}\)