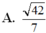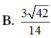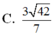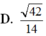Đáp án A
Gọi G là trọng tâm tam giác đều ABC suy ra G A ⊥ ( B C D )
Gọi M là trung điểm BD.
Đặt A C = x ⇒ G C = 2 3 C M = x 3 3
lại có A C 2 - G C 2 = A G 2
![]()
⇒ x = a 6 2
Đáp án A
Gọi G là trọng tâm tam giác đều ABC suy ra G A ⊥ ( B C D )
Gọi M là trung điểm BD.
Đặt A C = x ⇒ G C = 2 3 C M = x 3 3
lại có A C 2 - G C 2 = A G 2
![]()
⇒ x = a 6 2
Tứ diện đều ABCD có khoảng cách từ điểm A đến mặt phẳng (BCD) = a. Cạnh của tứ diện có độ dài bằng?
A. a 6 3
B. a 6 2
C. a 2 3
D. a 2 2
Cho tứ diện đều ABCD. Biết khoảng cách từ điểm A đến mặt phẳng (BCD) bằng 6. Tính thể tích của tứ diện ABCD
A. V = 27 3
B. C. V = 27 3 2 D. V = 9 3 2
C. V = 27 3 2
D. V = 9 3 2
Cho tứ diện đều ABCD có cạnh bằng a. Tính khoảng cách từ A đến mặt phẳng (BCD)?
A. a 6 2
B. a 6 3
C. 3 a 2
D. 2a
Cho tứ diện ABCD có AB = AD = a 2 , BC = BD = a và CA = CD = x. Khoảng cách từ B đến mặt phẳng (ACD) bằng a 3 2 . Biết thể tích của khối tứ diện bằng a 3 3 12 . Góc giữa hai mặt phẳng (ACD) và (BCD) là:
A.600
B.450
C.900
D.1200
Cho tứ diện ABCD có cạnh DA vuông góc với mặt phẳng (ABC) và AB=3cm, AC=4cm, AD= 6 CM, BC=5cm. Khoảng cách từ A đến mặt phẳng (BCD) bằng

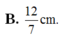

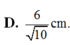
Cho tứ diện ABCD có đáy BCD 1à tam giác đều cạnh a và có thể tích V = a 3 3 2 . Khoảng cách từ A đến mặt phẳng (BCD) là.
A. a
B. 6a
C. 3a
D. 2a
Cho tứ diện ABCD có B A C ^ = C A D ^ = D A B ^ = 90 0 , A B = a , A C = 2 , A D = 3 . Khoảng cách từ A đến mặt phẳng (BCD) là
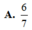
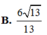
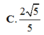
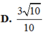
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC), AC = AD = 4, AB = 3, BC = 5. Tính khoảng cách từ điểm A đến mặt phẳng (BCD).
A. 34 12
B. 12 34
C. 769 60
D. 60 769
Tứ diện ABCD có AB=CD=4, AC=BD=5, AD=BC=6. Tính khoảng cách từ điểm A đến mặt phẳng (BCD).