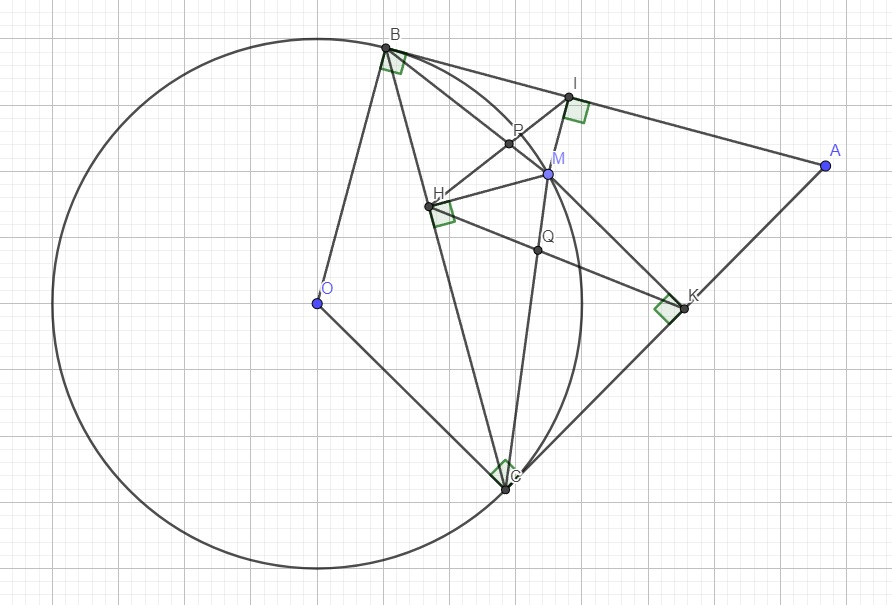
Từ điểm A ở bên ngoài đường tròn (O) kẻ hai tiếp tuyến AB và AC (B,C là các tiếp điểm). M là điểm bất kì trên cung nhỏ BC. Kẻ MI ⊥ AB, MH ⊥ BC, MK ⊥ AC(I,H,K là chân các đường vuông góc)
a) Chứng minh tứ giác BIMH nội tiếp
b) Chứng minh MH2 = MI . MK
***c) Gọi P là giao điểm của IH và MB. Q là giao điểm của KH và MC. Chứng minh MPHQ nội tiếp
a. Em tự giải
b.
THeo t/c hai tiếp tuyến cắt nhau \(AB=AC\Rightarrow\Delta ABC\) cân tại A
\(\Rightarrow\widehat{IBH}=\widehat{KCH}\)
H và K cùng nhìn CM dưới 1 góc vuông \(\Rightarrow CKMH\) nội tiếp
\(\Rightarrow\widehat{HMK}+\widehat{KCH}=180^0\)
BIMH nội tiếp \(\Rightarrow\widehat{IMH}+\widehat{IBH}=180^0\)
\(\Rightarrow\widehat{HMK}=\widehat{IMH}\) (1)
Cũng do CKMH nội tiếp \(\Rightarrow\widehat{MKH}=\widehat{MCH}\) (cùng chắn MH)
\(\widehat{MCH}=\widehat{IBM}\) (góc nt và góc tạo bởi tt - dây cung cùng chắn BM của (O))
\(\widehat{IBM}=\widehat{MHI}\) (cùng chắn IM)
\(\Rightarrow\widehat{MCH}=\widehat{MHI}\) (2)
\(\Rightarrow\widehat{MKH}=\widehat{MHI}\) (3)
(1);(3) \(\Rightarrow\Delta MKH\sim\Delta MHI\left(g.g\right)\)
\(\Rightarrow\dfrac{MH}{MI}=\dfrac{KM}{MH}\Rightarrow MH^2=MI.MK\)
c.
Theo (2): \(\widehat{MCH}=\widehat{MHI}\)
Lại có: \(\widehat{MHK}=\widehat{MCK}\) (cùng chắn MK của (CKMH))
\(\widehat{MCK}=\widehat{MBC}\) (cùng chắn MC của (O))
\(\Rightarrow\widehat{MHK}=\widehat{MBC}\)
Từ đó:
\(\widehat{PMQ}+\widehat{PHQ}=\widehat{PMQ}+\widehat{MHI}+\widehat{MHK}=\widehat{PMQ}+\widehat{MCH}+\widehat{MBC}=180^0\) (tổng 3 góc tam giác MBC)
\(\Rightarrow MPHQ\) nội tiếp