Hình vẽ:
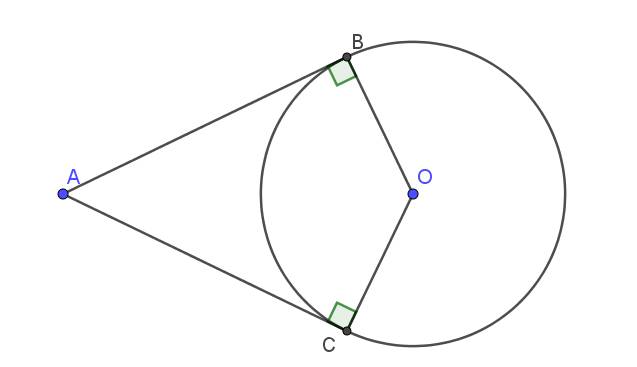
Vì $AB,AC$ là tiếp tuyến của $(O)$ nên $AB\perp OB, AC\perp OC$
$\Rightarrow \widehat{ABO}=\widehat{ACO}=90^0$
Tứ giác $ABOC$ có tổng hai góc đối nhau $\widehat{ABO}+\widehat{ACO}=90^0+90^0=180^0$
$\Rightarrow ABOC$ là tứ giác nội tiếp.
Hình vẽ:

Vì $AB,AC$ là tiếp tuyến của $(O)$ nên $AB\perp OB, AC\perp OC$
$\Rightarrow \widehat{ABO}=\widehat{ACO}=90^0$
Tứ giác $ABOC$ có tổng hai góc đối nhau $\widehat{ABO}+\widehat{ACO}=90^0+90^0=180^0$
$\Rightarrow ABOC$ là tứ giác nội tiếp.
Cho điểm A nằm ngoài đường tròn (O), qua A kẻ hai tiếp tuyến AB và AC với đường tròn ( B, C là tiếp điểm). Chứng minh tứ giác ABOC là tứ giác nội tiếp
:Cho đường tròn (O; R) và điểm A nằm ngoài đường tròn (O). Vẽ hai tiếp tuyến AB, AC của (O) (B, C là tiếp điểm). Vẽ cát tuyến ADE của (O) (D, E thuộc (O); D nằmgiữa Avà E; tia AD nằm giữa hai tia AB và AO). a) Chứng minh tứ giác ABOC nội tiếp được đường tròn và AB2 = AD. AE. b) Gọi H là giao điểm của OA và BC. Chứng minh tứ giác DEOH nội tiếp. c) Đường thẳng AO cắt đường tròn (O) tại M và N (M nằm giữa A và O). Chứng minh EH.AD = MH.AN.
cho đường tròn (O;R) A là điểm nằm bên ngoài đường tròn. Từ A kẻ 2 tiếp tuyến AB ,AC với đường tròn (O;R) (B và C là hai tiếp điểm)
a. Chứng minh tứ giác ABOC nội tiếp đường tròn
b. Kẻ cát tuyến AMN (M nằm giữa A và N). Chứng minh AB^2 = AM.AN
c. Gọi K là giao điểm của tia CM và AB. Chứng minh góc ABC = góc KMB
Cho đường tròn (O;R) và điểm A nằm ngoài đường tròn(O) vẽ hai tiếp tuyến AB, AC của (O) ( B và C là tiếp điểm), vẽ cát tuyến ADE của đường tròn (O) (D, E thuộc O) D nằm giữa A và E. Tia AD nằm giữa hai tia AB và AO
a. Chứng minh tứ giác ABOC nội tiếp đường tròn, xác định tâm của đường tròn ngoại tiếp
b.Gọi H là giao điểm của OA và BC chứng minh AB2 = AD.AE và AB2 = AH.AO
c. Đường thẳng AO cắt đường tròn (O) tại M và N (M nằm giữa A và O) Chứng minh EH.AD = MH.AN
Từ điểm A nằm ngoài đường tròn (O). Vẽ hai tiếp tuyến AB, AC với đường tròn (O) (B, C là hai tiếp điểm).
a) Chứng minh tứ giác ABOC nội tiếp được đường tròn.
b) Vẽ cát tuyến ADE của (O) sao cho cát tuyến ADE nằm giữa 2 tia AO, AB; D, E thuộc đường tròn (O) và D nằm giữa A, E. Chứng minh AB 2 =AD.AE .
c) Gọi F là điểm đối xứng của D qua AO, H là giao điểm của AO và BC. Chứng minh: ba điểm E, F, H thẳng hàng.
Cho đường tròn tâm \(O\). Từ điểm \(A\) nằm ngoài đường tròn vẽ hai tiếp tuyến \(AB,AC\). Đường thẳng \(AO\) cắt \(BC\) tại \(E\).
\(a\)) Chứng minh: Tứ giác \(ABOC\) nội tiếp.
\(b\)) Gọi \(I\) là trung điểm của \(BE\). Đường thẳng qua \(I\) và vuông góc với \(OI\) cắt \(AB,AC\) lần lượt tại \(D,F\). Chứng minh rằng: \(\widehat{IDO}=\widehat{BCO}\).
\(c\)) Chứng minh rằng: Tam giác \(ODF\) cân.
\(d\)) Chứng minh rằng: \(F\) là trung điểm của \(AC\).
Lấy Điểm A nằm ngoài đường tròn ( O;R) sao cho AO = 3R. Vẽ hai tiếp tuyến AB; AC với đường tròn ( B;C là tiếp điểm). a) Chứng minh: Tứ giác ABOC nội tiếp đường tròn. b) Qua A vẽ cát tuyến AEF với (O) sao cho E nằm giữa A và F và cắt đoạn thẳng OB tại K. Chứng minh: AC^2 = AE.AF c) Từ E vẽ đường thẳng vuông góc với OB cắt BC tại M, I là trung điểm của EF. Chứng minh: MI // FB.
Cho điểm A nằm ngoài đường tròn (O,R) từ A kẻ hai tiếp tuyến AB,AC và cát tuyến ADE( B,C là hai tiếp điểm ,O nằm trong góc BAE ) BC cắt OA tại I
a/Chứng minh Tứ giác ABOC nội tiếp và OA vuông góc với BC
b/Chứng minh OI.IA =BC^2/4 và AB.AC = AD.AE
c/Vẽ đường kính BK của (O),tia KD cắt OA tại F. Chứng minh FB vuông góc EB