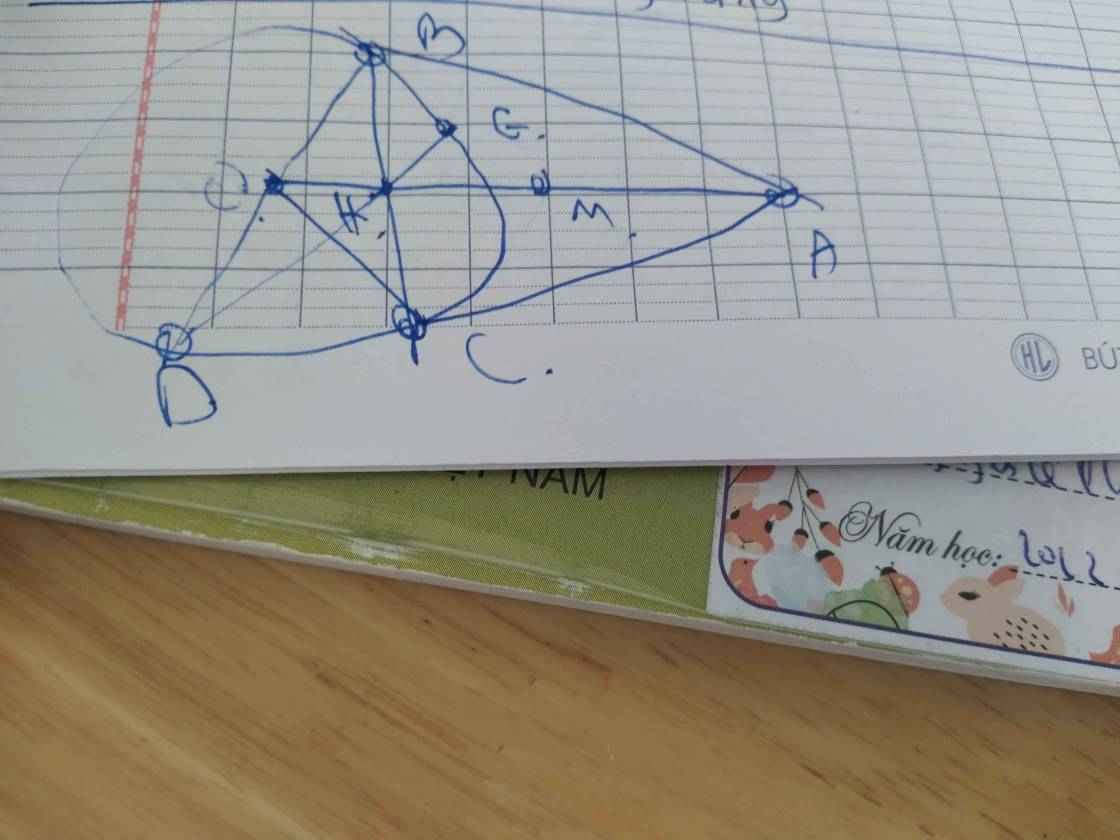
Từ điểm A nằm ngoài (O) vẽ 2 tiếp tuyến AB,AC với đường tròn trong đó B,C Là các tiếp điểma) chứng minh tứ giác ABOC nội tiếp và xác định tâm M đường tròn ngoại tiếp tứ giác nàyb) gọi H là giao của BC và OA . chứng minh AMC =BOC và HA.HO=HB.HCc) vẽ đường kính BD của (O), HD cắt (O)tại điểm thứ 2 là E . chứng minh AO là tia phân giác của DAEd)AD cắt (O) tại điểm thứ 2 là K , gọi F là hình chiếu của C lên DE .CHỨNG MINH KF vg với BCgiúp mình câu d ạ
Các câu hỏi tương tự
Từ điểm A nằm ngoài (O) vẽ 2 tiếp tuyến AB,AC với đường tròn trong đó B,C Là các tiếp điểma) chứng minh tứ giác ABOC nội tiếp và xác định tâm M đường tròn ngoại tiếp tứ giác nàyb) gọi H là giao của BC và OA . chứng minh AMC BOC và HA.HOHB.HCc) vẽ đường kính BD của (O), HD cắt (O)tại điểm thứ 2 là E . chứng minh AO là tia phân giác của DAEd)AD cắt (O) tại điểm thứ 2 là K , gọi F là hình chiếu của C lên DE .CHỨNG MINH KF vg với BC
Đọc tiếp
Từ điểm A nằm ngoài (O) vẽ 2 tiếp tuyến AB,AC với đường tròn trong đó B,C Là các tiếp điểma) chứng minh tứ giác ABOC nội tiếp và xác định tâm M đường tròn ngoại tiếp tứ giác nàyb) gọi H là giao của BC và OA . chứng minh AMC =BOC và HA.HO=HB.HCc) vẽ đường kính BD của (O), HD cắt (O)tại điểm thứ 2 là E . chứng minh AO là tia phân giác của DAEd)AD cắt (O) tại điểm thứ 2 là K , gọi F là hình chiếu của C lên DE .CHỨNG MINH KF vg với BC
từ điểm A nằm ngoài đường tròn (O) vẽ hai tiếp tuyến AB và AC đến đường tròn (O) (B,C là các tiếp điểm). Đường tròn I đường kính AB cắt BC tại H và cắt đường tròn O tại D (D khác B).b) gọi K là giao điểm của OI với BD. Chứng minh tứ giác AIKH nội tiếp.c) Đường tròn (I) cắt AC tại E. Gọi F là giao điểm của OA với BE. Chứng minh đường tròn ngoại tiếp tam giác ABF đi qua điểm K.
Đọc tiếp
từ điểm A nằm ngoài đường tròn (O) vẽ hai tiếp tuyến AB và AC đến đường tròn (O) (B,C là các tiếp điểm). Đường tròn I đường kính AB cắt BC tại H và cắt đường tròn O tại D (D khác B).
b) gọi K là giao điểm của OI với BD. Chứng minh tứ giác AIKH nội tiếp.
c) Đường tròn (I) cắt AC tại E. Gọi F là giao điểm của OA với BE. Chứng minh đường tròn ngoại tiếp tam giác ABF đi qua điểm K.
Cho tam giác ABC vuông tại A. Vẽ đường tròn (O) đường kính AB cắt BC tại Ha) Chứng minh AC là tiếp tuyến của (O) và BH.BC 4OB^2b Gọi D là điểm chính giữa cung AH, tiếp tuyến tại H với đường tròn (O) cắt AC tại M . chứng minh BD là phân giác của góc ABC và 3 điểm O,D,M thẳng hàng c) CHứng minh tứ giác OAHM nội tiếp và góc CMH 2.HOMd) Tia BD cắt AC tại E, gọi I là tâm đường tròn ngoại tiếp tam giác CDE. chứng minh IO vuông góc với HDe) Từ C vẽ tiếp tuyến Cx với đường tròn (O) , từ O vẽ tia Oy vu...
Đọc tiếp
Cho tam giác ABC vuông tại A. Vẽ đường tròn (O) đường kính AB cắt BC tại H
a) Chứng minh AC là tiếp tuyến của (O) và BH.BC = 4OB^2
b Gọi D là điểm chính giữa cung AH, tiếp tuyến tại H với đường tròn (O) cắt AC tại M . chứng minh BD là phân giác của góc ABC và 3 điểm O,D,M thẳng hàng
c) CHứng minh tứ giác OAHM nội tiếp và góc CMH = 2.HOM
d) Tia BD cắt AC tại E, gọi I là tâm đường tròn ngoại tiếp tam giác CDE. chứng minh IO vuông góc với HD
e) Từ C vẽ tiếp tuyến Cx với đường tròn (O) , từ O vẽ tia Oy vuông góc với OC. Gọi K là giao điểm của Cx và Oy. CHứng minh BK là tiếp tuyến của (O)
làm ơn giúp mình giải bài toán này mình đang cần gấp để nộp mình xin cảm ơn nhiều
Làm giúp mình 2 bài này với, mai mình phải nộp rồi!!!Bài 1: Từ điểm A nằm ngoài đường tròn (O;R), vẽ 2 tiếp tuyến AB, AC với đường tròn.a) Chứng minh tứ giác OBAC nội tiếp và OA vuông góc BC tại Hb) Vẽ đường kính CD của đường tròn (O;R), AD cắt (O) tại M. Chứng minh: góc BHM góc MACc) Tia BM cắt AO tại N. Chứng minh NANHd) Vẽ ME là đường kính đường tròn (O), gọi I là trung điểm DM. Chứng minh: 3 điểm B, I, E thẳng hàng và BI song song MH.Bài 2: Cho tam giác ABC vuông tại A. Vẽ đường tròn tâm O...
Đọc tiếp
Làm giúp mình 2 bài này với, mai mình phải nộp rồi!!!
Bài 1:
Từ điểm A nằm ngoài đường tròn (O;R), vẽ 2 tiếp tuyến AB, AC với đường tròn.
a) Chứng minh tứ giác OBAC nội tiếp và OA vuông góc BC tại H
b) Vẽ đường kính CD của đường tròn (O;R), AD cắt (O) tại M. Chứng minh: góc BHM = góc MAC
c) Tia BM cắt AO tại N. Chứng minh NA=NH
d) Vẽ ME là đường kính đường tròn (O), gọi I là trung điểm DM. Chứng minh: 3 điểm B, I, E thẳng hàng và BI song song MH.
Bài 2:
Cho tam giác ABC vuông tại A. Vẽ đường tròn tâm O đường kính AC cắt BC tại H. Gọi I là trung điểm của HC. Tia OI cắt (O) tại F
a) Chứng minh AH là đường cao của tam giác ABC và AB^2= BH. BC
b) Chứng minh: Tứ giác ABIO nội tiếp
c) Chứng minh: AF là tia phân giác của góc HAC
d) AF cắt BC tại D. Chứng minh: BA=BD
Cho đường tròn (O) bán kính R và điểm A nằm ngoài đường tròn (O). Vẽ 2 tiếp tuyết AB và AC của đường tròn (O) (B, C là tiếp điểm), OA cắt BC tại H
a) Chứng minh tứ giác ABOC nội tiếp và xác định M là đường tròn ngoại tiếp tứ giác này.
b) Chứng minh OA vuông góc BC
c) Vẽ cát tuyến AEF (AEF nằm giữa 2 tia AB, AO). Gọi K là trung điểm của EF. Chứng minh 5 điểm A, B, K, O, V cùng thuộc 1 đường tròn.
Đọc tiếp
Cho đường tròn (O) bán kính R và điểm A nằm ngoài đường tròn (O). Vẽ 2 tiếp tuyết AB và AC của đường tròn (O) (B, C là tiếp điểm), OA cắt BC tại H a) Chứng minh tứ giác ABOC nội tiếp và xác định M là đường tròn ngoại tiếp tứ giác này. b) Chứng minh OA vuông góc BC c) Vẽ cát tuyến AEF (AEF nằm giữa 2 tia AB, AO). Gọi K là trung điểm của EF. Chứng minh 5 điểm A, B, K, O, V cùng thuộc 1 đường tròn.
Cho đường tròn tâm O và điểm S nằm bên ngoài đường tròn (O). từ S kẻ 2 tiếp tuyến SA,SB với đường tòn (O),(A,B là các tiếp điểm). gọi D là giao điểm của AO và SB, E là giao điểm của SO và AB. Vẽ AD cắt đường tròn (O) tại điểm thứ 2 là C.kẻ BH vuông góc ACa/ chứng minh tứ giác SAOB là tứ giác nội tiếpb/ chứng minh BC // SO và BC là phân giác của góc HBDc/ gọi F là giao điểm của SC và BH. Chứng minh F là trung điểm của đoạn BH
Đọc tiếp
Cho đường tròn tâm O và điểm S nằm bên ngoài đường tròn (O). từ S kẻ 2 tiếp tuyến SA,SB với đường tòn (O),(A,B là các tiếp điểm). gọi D là giao điểm của AO và SB, E là giao điểm của SO và AB. Vẽ AD cắt đường tròn (O) tại điểm thứ 2 là C.kẻ BH vuông góc AC
a/ chứng minh tứ giác SAOB là tứ giác nội tiếp
b/ chứng minh BC // SO và BC là phân giác của góc HBD
c/ gọi F là giao điểm của SC và BH. Chứng minh F là trung điểm của đoạn BH
Cho điểm A nằm ngoài đường tròn (O; R), kẻ các tiếp tuyến AB, AC với (O) (B và C là các tiếp điểm). Vẽ đường kính CE của (O). Gọi H là giao điểm của OA và BC. a) Chứng minh tứ giác ABOC nội tiếp và BE // OA. b) AE cắt (O) tại D (khác E), BD cắt OA tại M. Chứng minh MAD MBA vàAH AC D D . c) Vẽ EI vuông góc với OA tại I; vẽ DK là đường kính của (O). Chứng minh 3 điểm K, I, B thẳng hàng.
Đọc tiếp
Cho điểm A nằm ngoài đường tròn (O; R), kẻ các tiếp tuyến AB, AC với (O) (B và C là các tiếp điểm). Vẽ đường kính CE của (O). Gọi H là giao điểm của OA và BC. a) Chứng minh tứ giác ABOC nội tiếp và BE // OA. b) AE cắt (O) tại D (khác E), BD cắt OA tại M. Chứng minh MAD MBA vàAH AC D D . c) Vẽ EI vuông góc với OA tại I; vẽ DK là đường kính của (O). Chứng minh 3 điểm K, I, B thẳng hàng.
Từ một điểm A ở bên ngoài đường tròn tâm O, kẻ hai tiếp tuyến AB và AC với đường tròn này (B VÀ C thuộc đường tròn tâm O)1) Chứng minh tứ giác ABOC nội tiếp đường tròn. Xác định tâm của đường tròn ngoại tiếp tứ giác ABOC.2) gọi D là trung điểm của đoạn thẳng Ac. Đoạn thẳng BD cắt đường tròn tâm O tại E ( E khác B ). Tia AE cắt đường tròn tâm O tại điểm F ( F khác E)3) gọi H là giao điểm của AO và BC. Chứng minh góc DHC bằng góc DEC.
Đọc tiếp
Từ một điểm A ở bên ngoài đường tròn tâm O, kẻ hai tiếp tuyến AB và AC với đường tròn này (B VÀ C thuộc đường tròn tâm O)
1) Chứng minh tứ giác ABOC nội tiếp đường tròn. Xác định tâm của đường tròn ngoại tiếp tứ giác ABOC.
2) gọi D là trung điểm của đoạn thẳng Ac. Đoạn thẳng BD cắt đường tròn tâm O tại E ( E khác B ). Tia AE cắt đường tròn tâm O tại điểm F ( F khác E)
3) gọi H là giao điểm của AO và BC. Chứng minh góc DHC bằng góc DEC.
Từ một điểm A ở bên ngoài đường tròn tâm O, kẻ hai tiếp tuyến AB và AC với đường tròn này (B và C thuộc đường tròn tâm O) 1) Chứng minh tứ giác ABOC nội tiếp đường tròn. Xác định tâm của đường tròn ngoại tiếp tứ giác ABOC. 2) Gọi D là trung điểm của đoạn thẳng AC . Đoạn thẳng BD cắt đường tròn tâm O tại E ( E khác B ). Tia AE cắt đường tròn tâm O tại điểm F ( F khác E) 3) Gọi H là giao điểm của AO và BC. Chứng minh góc DHC bằng góc DEC .
Đọc tiếp
Từ một điểm A ở bên ngoài đường tròn tâm O, kẻ hai tiếp tuyến AB và AC với đường tròn này (B và C thuộc đường tròn tâm O)
1) Chứng minh tứ giác ABOC nội tiếp đường tròn. Xác định tâm của đường tròn ngoại tiếp tứ giác ABOC.
2) Gọi D là trung điểm của đoạn thẳng AC . Đoạn thẳng BD cắt đường tròn tâm O tại E ( E khác B ). Tia AE cắt đường tròn tâm O tại điểm F ( F khác E)
3) Gọi H là giao điểm của AO và BC. Chứng minh góc DHC bằng góc DEC .