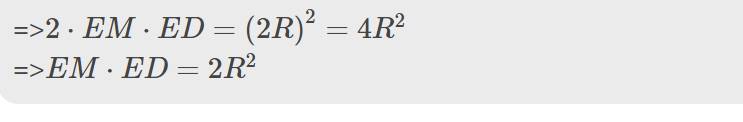Các câu hỏi tương tự
Từ A ngoài (O), bán kính R, vẽ tiếp tuyến AE và dây EF vuông góc với OA tại M
a) cho R =10cm,OM =6cm. Tính EF
b) c/m AF là tiếp tuyến của (O)
c) kẻ đường kính EC, tiếp tuyến với (O) tại C cắt EF tại D. Tính EM.ED theo R
d) kẻ tiếp tuyến DB. c/m A,B,C thẳng hàng
Câu 1: Cho (O;R) và điểm A nằm ngoài đường tròn (O). Vẽ 2 tiếp tuyến AB, AC của (O) (B,C: tiếp điểm). Vẽ cát tuyến ADE của (O); D nằm giữa D & E; tia AD nằm giữa 2 tia AB và AO.a) Gọi H là giao điểm của OA và BC. C/m: DEOH nội tiếpb) Đường thẳng AO cắt (O) tại M và N (M nằm giữa A và O). C/m: EH.AD MH.ANCâu 2: Cho nửa đường tròn tâm (O;R) đường kính AB và điểm C trên đường tròn sao cho CACB. Gọi M là trung điểm của dây cung AC. Nối BM cắt cung AC tại E; AE và BC kéo dài cắt nhau tại D.a) C/m: MO...
Đọc tiếp
Câu 1: Cho (O;R) và điểm A nằm ngoài đường tròn (O). Vẽ 2 tiếp tuyến AB, AC của (O) (B,C: tiếp điểm). Vẽ cát tuyến ADE của (O); D nằm giữa D & E; tia AD nằm giữa 2 tia AB và AO.
a) Gọi H là giao điểm của OA và BC. C/m: DEOH nội tiếp
b) Đường thẳng AO cắt (O) tại M và N (M nằm giữa A và O). C/m: EH.AD= MH.AN
Câu 2: Cho nửa đường tròn tâm (O;R) đường kính AB và điểm C trên đường tròn sao cho CA=CB. Gọi M là trung điểm của dây cung AC. Nối BM cắt cung AC tại E; AE và BC kéo dài cắt nhau tại D.
a) C/m: MOCD là hình bình hành
b) Vẽ đường tròn tâm E bán kính EA cắt (O) tại điểm thứ 2 là N. Kẻ EF vuông góc với AC, EF cắt AN tại I, cắt (O) tại điểm thứ 2 là K; EB cắt AN tại H. C/m: BHIK nội tiếp.
Câu 3: Cho (O;R). Từ điểm S nằm ngoài đường tròn sao cho SO=2R. Vẽ tiếp tuyến SA,SB (A,B là tiếp tuyến). Vẽ cát tuyến SDE (D nằm giữa S và E), điểm O nằm trong góc ESB. Từ O kẻ đường vuông góc với OA cắt SB tại M. Gọi I là giao điểm của OS và (O).
a) C/m: MI là tiếp tuyến của (O)
b) Qua D kẻ đường vuông góc với OB cắt AB tại H và EB tại K. C/m: H là trung điểm của DK.
Cho đường tròn (O;R) và điểm A với OA2R . Từ A vẽ 2 tiếp tuyến AE, AF đến (O) (E , F là 2 tiếp điểm). Đường thẳng OA cắt (O) tại C và D (O nằm giữa A và C)a) Tính diện tích tứ giác AECF theo Rb) Từ O vẽ đt vuông góc với OE cắt AF tại M. Tính tỉ số diện tích 2 tam giác OAM và ÒMc) Đường thẳng kẻ từ D vuông góc với OE cắt EC tại Q. c/m các đường thẳng AC,EF,QM đồng quy.
Đọc tiếp
Cho đường tròn (O;R) và điểm A với OA=2R . Từ A vẽ 2 tiếp tuyến AE, AF đến (O) (E , F là 2 tiếp điểm). Đường thẳng OA cắt (O) tại C và D (O nằm giữa A và C)
a) Tính diện tích tứ giác AECF theo R
b) Từ O vẽ đt vuông góc với OE cắt AF tại M. Tính tỉ số diện tích 2 tam giác OAM và ÒM
c) Đường thẳng kẻ từ D vuông góc với OE cắt EC tại Q. c/m các đường thẳng AC,EF,QM đồng quy.
Cho đường tròn tâm O bán kính R và một điểm M sao cho OM2R,từ M kẻ hai tiếp tuyến MA,MB của đường tròn tâm O bán kính R (A,B là tiếp điểm).a)Chứng minh tam giác MAB đều,tính AM theo Rb)Qua điểm C thuộc ucng nhỏ AB vẽ tiếp tuyến với đường tròn tâm O bán kính R cắt MA tại E,cắt MB tại F,OF cắt AB tại K,OE cắt AB tại H.Chứng minh EK vuống góc với OFc)Khi số đo cung BC90 độ.Tính EF và diện tích tam giác OHK theo R
Đọc tiếp
Cho đường tròn tâm O bán kính R và một điểm M sao cho OM=2R,từ M kẻ hai tiếp tuyến MA,MB của đường tròn tâm O bán kính R (A,B là tiếp điểm).
a)Chứng minh tam giác MAB đều,tính AM theo R
b)Qua điểm C thuộc ucng nhỏ AB vẽ tiếp tuyến với đường tròn tâm O bán kính R cắt MA tại E,cắt MB tại F,OF cắt AB tại K,OE cắt AB tại H.Chứng minh EK vuống góc với OF
c)Khi số đo cung BC=90 độ.Tính EF và diện tích tam giác OHK theo R
cho(O;R) và điểm A nằm ngoài đường tròn.Qua A kẻ tiếp tuyến AB với (O;R) (B là tiếp điểm),Tia Ax nằm giữa AB và AO cắt (O)tại C và D .(C nằm giữa A và D).M là trung điểm của dây CD,kẻ BH vuông góc với AO tại H.a,Tính OH,OA theo R.b,Chứng minh 4 điểm A,B,M,O cùng thuộc một đường tròn.c,Gọi E là giao điểm của OM và HB.Chứng minh EC là tiếp tuyến của (O;R)
Cho (O; R) có đường kính AB. Lấy điểm C trên đường tròn sao cho AC R.a) Tính BC theo R và các góc của ΔABC.b) Gọi M là trung điểm của OA. Vẽ dây CD vuông góc với AB tại M. Chứngminh: tứ giác ACOD là hình thoi.c) Tiếp tuyến tại C của đường tròn cắt đường thẳng AB tại E. Chứng minh: EDlà tiếp tuyến của (O).d) Hai đường thẳng EC và DO cắt nhau tại F. Chứng minh: C là trung điểm của EF
Đọc tiếp
Cho (O; R) có đường kính AB. Lấy điểm C trên đường tròn sao cho AC = R.
a) Tính BC theo R và các góc của ΔABC.
b) Gọi M là trung điểm của OA. Vẽ dây CD vuông góc với AB tại M. Chứng
minh: tứ giác ACOD là hình thoi.
c) Tiếp tuyến tại C của đường tròn cắt đường thẳng AB tại E. Chứng minh: ED
là tiếp tuyến của (O).
d) Hai đường thẳng EC và DO cắt nhau tại F. Chứng minh: C là trung điểm của EF
từ điểm M nằm ngoài (O),kẻ tiếp tuyến MA với (O) (A là tiếp điểm ).Từ A kẻ đường thẳng vuông góc với OM tại H và cắt (O) tại B (B khác A).kẻ đường kính AC của (O).Tiếp tuyến tại C của (O) cắt đường thẳng AB tại Ea,c/minh 4 điểm E,H,O,C cùng thuộc một đường trònb,chứng minh △△ ABC cânc,Chứng minh BE.BMBC.BO
Đọc tiếp
từ điểm M nằm ngoài (O),kẻ tiếp tuyến MA với (O) (A là tiếp điểm ).Từ A kẻ đường thẳng vuông góc với OM tại H và cắt (O) tại B (B khác A).kẻ đường kính AC của (O).Tiếp tuyến tại C của (O) cắt đường thẳng AB tại Ea,c/minh 4 điểm E,H,O,C cùng thuộc một đường trònb,chứng minh ABC cânc,Chứng minh BE.BM=BC.BO
từ điểm M nằm ngoài (O),kẻ tiếp tuyến MA với (O) (A là tiếp điểm ).Từ A kẻ đường thẳng vuông góc với OM tại H và cắt (O) tại B (B khác A).kẻ đường kính AC của (O).Tiếp tuyến tại C của (O) cắt đường thẳng AB tại E
a,c/minh 4 điểm E,H,O,C cùng thuộc một đường tròn
b,chứng minh \(\Delta ABC\) cân
c,Chứng minh BE.BM=BC.BO
Đường tròn (O) , bán kính R , A nằm ngoài đường tròn, OA=2R . Vẽ tiếp tuyến AB của đường tròn
â) CM: Tam giác OAB vg tại B , tính AB theo R
b) Từ B kẻ dây cung vuông góc OA tại H . CM: AC là tiếp tuyến (O)
c) CM: tam giác ABC đều
đ) Từ H vẽ đường thẳng vuông góc AB tại D, đường tròn đường kính AC cắt CD tại E. CM: A,E,F thẳng hàng