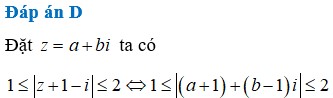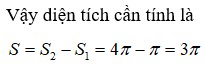Các câu hỏi tương tự
Trong mặt phẳng phức Oxy, tập hợp biểu diễn số phức z thỏa
1
≤
z
+
1
−
i
≤
2
là hình vành khăn. Diện tích S của hình vành khăn là bao nhiêu ? A.
S
4
π
B.
S
π
C.
S
2
π
D. ...
Đọc tiếp
Trong mặt phẳng phức Oxy, tập hợp biểu diễn số phức z thỏa 1 ≤ z + 1 − i ≤ 2 là hình vành khăn. Diện tích S của hình vành khăn là bao nhiêu ?
A. S = 4 π
B. S = π
C. S = 2 π
D. S = 3 π
Tập hợp tất cả các điểm biểu diễn số phức z thỏa mãn
1
≤
z
≤
2
là một hình vành khăn có diện tích bằng A.
5
π
B.
π
C.
3
π
D.
4
π
Đọc tiếp
Tập hợp tất cả các điểm biểu diễn số phức z thỏa mãn 1 ≤ z ≤ 2 là một hình vành khăn có diện tích bằng
A. 5 π
B. π
C. 3 π
D. 4 π
Cho số phức z thỏa mãn điều kiện
z
-
3
+
4
i
≤
2
.
Trong mặt phẳng Oxy, tập hợp điểm biểu diễn số phức w 2z + 1 - i là hình tròn có diện tích bằng A.
S
25
π
B.
S
4
π
C.
S
16
π...
Đọc tiếp
Cho số phức z thỏa mãn điều kiện z - 3 + 4 i ≤ 2 . Trong mặt phẳng Oxy, tập hợp điểm biểu diễn số phức w = 2z + 1 - i là hình tròn có diện tích bằng
A. S = 25 π
B. S = 4 π
C. S = 16 π
D. S = 9 π
Trong mặt phẳng tọa độ Oxy, gọi (H) là tập hợp điểm biểu diễn số phức
w
(
1
+
3
i
)
z
+
2
thỏa mãn
|
z
-
1
|
≤
2
. Tính diện tích của hình (H). A. 8
π
.
...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, gọi (H) là tập hợp điểm biểu diễn số phức w = ( 1 + 3 i ) z + 2 thỏa mãn | z - 1 | ≤ 2 . Tính diện tích của hình (H).
A. 8 π .
B. 12 π .
C. 16 π .
D. 4 π .
Cho số phức z thỏa mãn điều kiện
3
≤
z
−
3
i
+
1
≤
5.
Tập hợp các điểm biểu diễn của Z tạo thành một hình phẳng. Tính diện tích S của hình phẳng đó. A.
S
25
π
.
B.
S
8
π
.
C.
S
4
π
....
Đọc tiếp
Cho số phức z thỏa mãn điều kiện 3 ≤ z − 3 i + 1 ≤ 5. Tập hợp các điểm biểu diễn của Z tạo thành một hình phẳng. Tính diện tích S của hình phẳng đó.
A. S = 25 π .
B. S = 8 π .
C. S = 4 π .
D. S = 16 π .
Cho số phức z thỏa mãn điều kiện
z
+
4
+
z
-
4
10
Tập hợp điểm biểu diễn số phức z trong mặt phẳng tọa độ Oxy là một hình phẳng có diện tích bằng A. 20
π
B. 15
π
C. 12
π
D. 16
π
Đọc tiếp
Cho số phức z thỏa mãn điều kiện z + 4 + z - 4 = 10 Tập hợp điểm biểu diễn số phức z trong mặt phẳng tọa độ Oxy là một hình phẳng có diện tích bằng
A. 20 π
B. 15 π
C. 12 π
D. 16 π
Cho hai số phức z, w thay đổi thỏa mãn
z
3
,
z
−
w
1
. Biết tập hợp điểm của số phức w là hình phẳng H. Tính diện tích S của hình H. A.
S
20
π
B.
S
12
π
C.
S
4
π
D.
S
16
π
Đọc tiếp
Cho hai số phức z, w thay đổi thỏa mãn z = 3 , z − w = 1 . Biết tập hợp điểm của số phức w là hình phẳng H. Tính diện tích S của hình H.
A. S = 20 π
B. S = 12 π
C. S = 4 π
D. S = 16 π
Cho số phức z thỏa mãn điều kiện
z
−
3
+
4
i
≤
2
. Trong mặt phẳng tọa độ, tập hợp điểm biểu diễn số phức
w
2
z
+
1
−
i
là hình tròn có diện tích A.
9
π
B.
12
π
C.
16
π
D.
25...
Đọc tiếp
Cho số phức z thỏa mãn điều kiện z − 3 + 4 i ≤ 2 . Trong mặt phẳng tọa độ, tập hợp điểm biểu diễn số phức w = 2 z + 1 − i là hình tròn có diện tích
A. 9 π
B. 12 π
C. 16 π
D. 25 π
Trong mặt phẳng tọa độ Oxy, gọi (H) là phần mặt phẳng chứ các điểm biểu diễn các số phức z thỏa mãn
z
16
và
16
z
có phần thực và phần ảo đều thuộc đoạn [0;1]. Tính diện tích S của (H) A.
S
32
6
-
π
B.
S
16
4
-
π...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, gọi (H) là phần mặt phẳng chứ các điểm biểu diễn các số phức z thỏa mãn z 16 và 16 z có phần thực và phần ảo đều thuộc đoạn [0;1]. Tính diện tích S của (H)
A. S = 32 6 - π
B. S = 16 4 - π
C. S = 256
D. S = 64 π