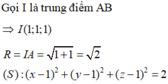Các câu hỏi tương tự
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1; 2; 3), B(-1; 4; 1). Viết phương trình mặt cầu (S) đường kính AB A.
(
S
)
:
x
2
+
(
y
-
3
)
2
+
(
z
-
2
)
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1; 2; 3), B(-1; 4; 1). Viết phương trình mặt cầu (S) đường kính AB
A. ( S ) : x 2 + ( y - 3 ) 2 + ( z - 2 ) 2 = 3
B. ( S ) : ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 12
C. ( S ) : ( x + 1 ) 2 + ( y - 4 ) 2 + ( z - 1 ) 2 = 12
D. ( S ) : x 2 + ( y - 3 ) 2 + ( z - 2 ) 2 = 12
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(0; 1; 2) và B(2;-l;4). Phương trình mặt cầu đường kính AB là A.
x
+
1
2
+
y
2
+
z
+
3
2
3
B.
x
2
+...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(0; 1; 2) và B(2;-l;4). Phương trình mặt cầu đường kính AB là
A. x + 1 2 + y 2 + z + 3 2 = 3
B. x 2 + y - 1 2 + z - 3 2 = 3
C. x - 1 2 + y 2 + z - 3 2 = 3
D. x - 1 2 + y 2 + z - 3 2 = 3
Trong không gian tọa độ Oxyz, cho mặt cầu (S) có phương trình (x-2)2 + (y+1)2 + (z-3)2 20. Mặt phẳng có phương trình x-2y+2z-10 và đường thẳng
∆
có phương trình
x
1
y
+
2
2
z
+
4
-
30
.
Viết phương trình đường thẳng ...
Đọc tiếp
Trong không gian tọa độ Oxyz, cho mặt cầu (S) có phương trình (x-2)2 + (y+1)2 + (z-3)2 = 20. Mặt phẳng có phương trình x-2y+2z-1=0 và đường thẳng ∆ có phương trình x 1 = y + 2 2 = z + 4 - 30 . Viết phương trình đường thẳng ∆ ' nằm trong mặt phẳng α vuông góc với ∆ đồng thời cắt (S) theo một dây cung có độ dài lớn nhất.
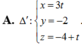

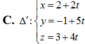
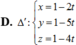
Trong không gian với hệ tọa độ Oxyz, viết phương trình chính tắc của mặt cầu có đường kính AB với A(2;1;0), B(0;1;2) A.
x
-
1
2
+
y
-
1
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, viết phương trình chính tắc của mặt cầu có đường kính AB với A(2;1;0), B(0;1;2)
A. x - 1 2 + y - 1 2 + z - 1 2 = 2
B. x + 1 2 + y + 1 2 + z + 1 2 = 2
C. x - 1 2 + y - 1 2 + z - 1 2 = 4
D. x + 1 2 + y + 1 2 + z + 1 2 = 4
Trong không gian với hệ tọa độ Oxyz, cho điểm
A
1
;
3
;
-
2
và mặt phẳng (P) có phương trình
(
P
)
:
2
x
-
y
+
2
z
-
1
0
. Viết phương trình mặt cầu (S) có tâm A và tiếp xúc với mặt phẳng (P). Tọa độ tiếpđiểm là: A.
H
7...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm
A 1 ; 3 ; - 2 và mặt phẳng (P) có phương trình
( P ) : 2 x - y + 2 z - 1 = 0 . Viết phương trình mặt cầu (S)
có tâm A và tiếp xúc với mặt phẳng (P). Tọa độ tiếp
điểm là:
A. H 7 3 ; 7 3 ; - 2 3
B. H 1 3 ; 1 3 ; - 2 3
C. H 7 3 ; - 7 3 ; 2 3
D. H 7 3 ; 7 3 ; 2 3
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
(
S
)
:
(
x
-
1
)
2
+
y
2
+
(
z
-
2
)
2
9
. Mặt phẳng tiếp xúc với mặt cầu (S) tại điểm
A
(
1
;
3
;
2
)
có phương trình là...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu ( S ) : ( x - 1 ) 2 + y 2 + ( z - 2 ) 2 = 9 . Mặt phẳng tiếp xúc với mặt cầu (S) tại điểm A ( 1 ; 3 ; 2 ) có phương trình là
A . x + y - 4 = 0
B . y - 3 = 0
C . 3 y - 1 = 0
D . x - 1 = 0
Trong không gian với hệ trục tọa độ Oxyz, cho các điểm
A
(
a
;
0
;
0
)
,
B
(
0
;
b
;
0
)
,
C
(
0
;
0
;
c
)...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A ( a ; 0 ; 0 ) , B ( 0 ; b ; 0 ) , C ( 0 ; 0 ; c ) , trong đó a > 0 , b > 0 , c > 0 và 3 a + 1 b + 3 c = 5 . Biết mặt phẳng (ABC) tiếp xúc với mặt cầu (S) có phương trình là ( x - 3 ) 2 + ( y - 1 ) 2 + ( z - 3 ) 2 = 304 25 , khi đó thể tích của khối tứ diện OABC nằm trong khoảng nào?
A . ( 0 ; 1 2 ) .
B. (0;1).
C. (1;3).
D. (4;5).
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d:
x
1
y
-
1
2
z
+
2
2
mặt phẳng (P): 2x+y+2z-50 và điểm A(1; 1; -2) Phương trình chính tắc của đường thẳng
∆
đi qua A song song với mặt phẳng (P) và vuông góc với d là A.
∆
:...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: x 1 = y - 1 2 = z + 2 2 mặt phẳng (P): 2x+y+2z-5=0 và điểm A(1; 1; -2) Phương trình chính tắc của đường thẳng ∆ đi qua A song song với mặt phẳng (P) và vuông góc với d là
A. ∆ : x - 1 1 = y - 1 2 = z + 2 - 2
B. ∆ : x - 1 2 = y - 1 1 = z + 2 - 2
C. ∆ : x - 1 2 = y - 1 2 = z + 2 - 3
D. ∆ : x - 1 1 = y - 2 2 = z + 2 2
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
S
:
x
−
2
2
+
y
−
1
2
+
z
2
1...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x − 2 2 + y − 1 2 + z 2 = 1 và mặt phẳng Q : 2 x − 2 y − z + 1 = 0 . Viết phương trình mặt cầu (S') đối xứng với mặt cầu (S) qua mặt phẳng (Q)
A. x + 2 3 2 + y − 7 3 2 + z − 2 3 2 = 1
B. x − 2 3 2 + y − 7 3 2 + z + 2 3 2 = 1
C. x − 2 3 2 + y + 7 3 2 + z − 2 3 2 = 1
D. x − 2 3 2 + y − 7 3 2 + z − 2 3 2 = 1
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x-2y+2z-20 và điểm I(-1;2;-1). Viết phương trình mặt cầu (S) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường tròn có bán kính bằng 5 A.
(
S
)
:
(
x
-
1
)
2
+
(
y
+
2
)
2
+
(
z
-
1
)
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x-2y+2z-2=0 và điểm I(-1;2;-1). Viết phương trình mặt cầu (S) có tâm I và cắt mặt phẳng (P) theo giao tuyến là đường tròn có bán kính bằng 5
A. ( S ) : ( x - 1 ) 2 + ( y + 2 ) 2 + ( z - 1 ) 2 = 34
B. ( S ) : ( x + 1 ) 2 + ( y - 2 ) 2 + ( z + 1 ) 2 = 16
C. ( S ) : ( x + 1 ) 2 + ( y - 2 ) 2 + ( z + 1 ) 2 = 25
D. ( S ) : ( x + 1 ) 2 + ( y - 2 ) 2 + ( z + 1 ) 2 = 34