Các câu hỏi tương tự
Trong không gian với hệ tọa độ Oxyz, cho hai véctơ
a
→
(2;-3;1) và (-1;0;4). Tìm tọa độ véctơ
u
→
-2
a
→
+3. A.(-7;6;-10) B.(-7;6;10) C.(7;6;10) D.(-7;-6;10)
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai véctơ
a
→
=(2;-3;1) và ![]() =(-1;0;4). Tìm tọa độ véctơ
u
→
=-2
a
→
+3
=(-1;0;4). Tìm tọa độ véctơ
u
→
=-2
a
→
+3![]() .
.
A.![]() =(-7;6;-10)
=(-7;6;-10)
B.![]() =(-7;6;10)
=(-7;6;10)
C.![]() =(7;6;10)
=(7;6;10)
D.![]() =(-7;-6;10)
=(-7;-6;10)
Trong không gian với hệ trục tọa độ Oxyz, cho véctơ
a
→
(
1
;
-
2
;
3
)
. Tìm tọa độ của véctơ
b
→
biết rằng véctơ ...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho véctơ a → = ( 1 ; - 2 ; 3 ) . Tìm tọa độ của véctơ b → biết rằng véctơ b → ngược hướng với véctơ a → và b → = 2 a →
A. b → =(2;-2;3)
B. b → =(2;-4;-6)
C. b → =(-2;4;-6)
D. b → =(-2;02;3)
Trong không gian với hệ tọa độ Oxyz, cho hai điểm
A
(
1
;
-
1
;
2
)
và
B
(
2
;
1
;
-
4
)
. Véctơ
A
B
→
có tọa độ là
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A ( 1 ; - 1 ; 2 ) và B ( 2 ; 1 ; - 4 ) . Véctơ A B → có tọa độ là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2;3;4) và B(5;1;1). Tìm tọa độ véctơ
A
B
→
A.
A
B
→
(3;2;3) B.
A
B
→
(3;-2;-3) C. ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2;3;4) và B(5;1;1). Tìm tọa độ véctơ A B →
A. A B → =(3;2;3)
B. A B → =(3;-2;-3)
C. A B → =(-3;2;3)
D. A B → =(3;-2;3)
Trong không gian với hệ trục tọa độ Oxyz, cho hai véctơ
u
→
2
;
3
;
-
1
và
v
→
5
;
-
4
;
m
. Tìm m để
u
→...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai véctơ u → = 2 ; 3 ; - 1 và v → = 5 ; - 4 ; m . Tìm m để u → ⊥ v →
A. - 2
B. 2
C. 4
D. 0
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A (1;1;0), B (0;-1;2). Biết rằng có hai mặt phẳng cùng đi qua hai điểm A, O và cùng cách B một khoảng bằng √3. Véctơ nào trong các véctơ dưới đây là một véctơ pháp tuyến của một trong hai mặt phẳng đó.
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A (1;1;0), B (0;-1;2). Biết rằng có hai mặt phẳng cùng đi qua hai điểm A, O và cùng cách B một khoảng bằng √3. Véctơ nào trong các véctơ dưới đây là một véctơ pháp tuyến của một trong hai mặt phẳng đó.
![]()
![]()
![]()
![]()
Trong không gian Oxyz, véctơ
u
→
vuông góc với hai véctơ
a
→
1
;
1
;
1
và
b
→
1
;
-
1
;
3
; đồng thời
u...
Đọc tiếp
Trong không gian Oxyz, véctơ u → vuông góc với hai véctơ a → = 1 ; 1 ; 1 và b → = 1 ; - 1 ; 3 ; đồng thời u → tạo với tia Oz một góc tù và độ dài véctơ u → bằng 3. Tìm véctơ u → .
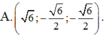
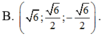
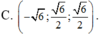
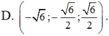
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;2;3), B(-2,1,5). Véctơ nào dưới đây là véctơ pháp tuyến của mặt phẳng (OAB).
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;2;3), B(-2,1,5). Véctơ nào dưới đây là véctơ pháp tuyến của mặt phẳng (OAB).
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) có phương trình 2x + 3y - 4z + 7= 0. Tìm tọa độ véctơ pháp tuyến của (P).
A. (-2;3;-4)
B. (-2;-3;-4)
C. (2;3;-4)
D. (2;-3;-4)



