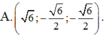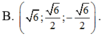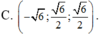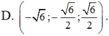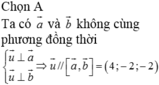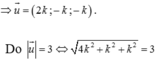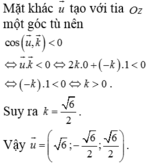Các câu hỏi tương tự
Tìm véctơ
u
→
biết rằng véctơ
u
→
vuông góc với véctơ
a
→
(1;-2;1) và thỏa mãn
u
→
.
b
→
-
1
,
u
→
.
c
→
-
5
với
b
→
(4;-5;2),
c...
Đọc tiếp
Tìm véctơ u → biết rằng véctơ u → vuông góc với véctơ a → (1;-2;1) và thỏa mãn u → . b → = - 1 , u → . c → = - 5 với b → (4;-5;2), c → =(8;4;-5)
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho hai véctơ
a
→
(2;-3;1) và (-1;0;4). Tìm tọa độ véctơ
u
→
-2
a
→
+3. A.(-7;6;-10) B.(-7;6;10) C.(7;6;10) D.(-7;-6;10)
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai véctơ
a
→
=(2;-3;1) và ![]() =(-1;0;4). Tìm tọa độ véctơ
u
→
=-2
a
→
+3
=(-1;0;4). Tìm tọa độ véctơ
u
→
=-2
a
→
+3![]() .
.
A.![]() =(-7;6;-10)
=(-7;6;-10)
B.![]() =(-7;6;10)
=(-7;6;10)
C.![]() =(7;6;10)
=(7;6;10)
D.![]() =(-7;-6;10)
=(-7;-6;10)
Trong không gian Oxyz, cho hai điểm M (-2;-2;1), A (1;2;-3) và đường thẳng
d
:
x
+
1
2
y
-
5
2
z
-
1
.Tìm véctơ chỉ phương
u
→
của đường thẳng Δ đi qua M, vuông góc với đường thẳng...
Đọc tiếp
Trong không gian Oxyz, cho hai điểm M (-2;-2;1), A (1;2;-3) và đường thẳng d : x + 1 2 = y - 5 2 = z - 1 .Tìm véctơ chỉ phương u → của đường thẳng Δ đi qua M, vuông góc với đường thẳng d, đồng thời cách điểm A một khoảng lớn nhất.
![]()
![]()
![]()
![]()
Trong không gian Oxyz cho hai điểm M(-2;-2;1), A(1;2;-3) và đường thẳng
d
:
x
+
1
2
y
-
5
2
z
-
1
. Tìm véctơ chỉ phương
u
→
của đường thẳng
∆
đi qua M, vuông gó...
Đọc tiếp
Trong không gian Oxyz cho hai điểm M(-2;-2;1), A(1;2;-3) và đường thẳng d : x + 1 2 = y - 5 2 = z - 1 . Tìm véctơ chỉ phương u → của đường thẳng ∆ đi qua M, vuông góc với đường thẳng d, đồng thời cách điểm A một khoảng lớn nhất.
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz cho hai véctơ
a
→
(
2
;
-
3
;
1
)
và
b
→
(
-
1
;
0
;
4
)
Tìm tọa độ vé...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho hai véctơ a → = ( 2 ; - 3 ; 1 ) và b → = ( - 1 ; 0 ; 4 ) Tìm tọa độ véctơ u → = - 2 a → + 3 b →
A. u → = ( - 7 ; 6 ; - 10 )
B. u → = ( - 7 ; 6 ; 10 )
C. u → = ( 7 ; 6 ; 10 )
D. u → = ( - 7 ; - 6 ; 10 )
Trong không gian Oxyz, cho hình lăng trụ tam giác đều ABC.A’B’C’ có
A
3
;
-
1
;
1
, hai đỉnh B, C thuộc trục Oz và AA’1 (C không trùng với O). Biết véctơ
u
→
a
;
b
;
2
với...
Đọc tiếp
Trong không gian Oxyz, cho hình lăng trụ tam giác đều ABC.A’B’C’ có A ' 3 ; - 1 ; 1 , hai đỉnh B, C thuộc trục Oz và AA’=1 (C không trùng với O). Biết véctơ u → = a ; b ; 2 với a , b ∈ ℝ là một véctơ chỉ phương của đường thẳng A’C. Tính T = a 2 + b 2
A. 5
B. 16
C. 4
D. 9
Trong không gian với hệ trục tọa độ Oxyz, cho hai véctơ
u
→
2
;
3
;
-
1
và
v
→
5
;
-
4
;
m
. Tìm m để
u
→...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai véctơ u → = 2 ; 3 ; - 1 và v → = 5 ; - 4 ; m . Tìm m để u → ⊥ v →
A. - 2
B. 2
C. 4
D. 0
Trong không gian với hệ trục tọa độ Oxyz, cho véctơ
a
→
(
1
;
-
2
;
3
)
. Tìm tọa độ của véctơ
b
→
biết rằng véctơ ...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho véctơ a → = ( 1 ; - 2 ; 3 ) . Tìm tọa độ của véctơ b → biết rằng véctơ b → ngược hướng với véctơ a → và b → = 2 a →
A. b → =(2;-2;3)
B. b → =(2;-4;-6)
C. b → =(-2;4;-6)
D. b → =(-2;02;3)
Trong không gian Oxyz cho đường thẳng
d
:
x
2
y
2
z
+
3
-
1
và mặt cầu
(
S
)
:
(
x
-
3
)
2...
Đọc tiếp
Trong không gian Oxyz cho đường thẳng d : x 2 = y 2 = z + 3 - 1 và mặt cầu ( S ) : ( x - 3 ) 2 + ( y - 2 ) 2 + ( z - 5 ) 2 = 36 . Gọi △ là đường thẳng đi qua A(2;1;3), vuông góc với đường thẳng d và cắt (S) tại hai điểm có khoảng cách lớn nhất. Khi đó đường thằng △ có một véctơ chỉ phương là u → = ( 1 ; a ; b ) . Tính
A. 4
B. -2
C. - 1 2
D. 5