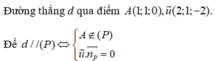Các câu hỏi tương tự
Trong không gian với hệ toạ độ Oxyz, cho điểm A(1;-2;3) và hai mặt phẳng (P):x+y+z+10;(Q):x-y+z-20. Phương trình nào dưới đây là phương trình đường thẳng qua A, song song với (P) và (Q). A.
x
1
+
2
t
y
-
2...
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho điểm A(1;-2;3) và hai mặt phẳng (P):x+y+z+1=0;(Q):x-y+z-2=0. Phương trình nào dưới đây là phương trình đường thẳng qua A, song song với (P) và (Q).
A. x = 1 + 2 t y = - 2 z = 3 + 2 t
B. x = - 1 + t y = 2 z = - 3 - t
C. x = 1 y = - 2 z = 3 - 2 t
D. x = 1 + t y = - 2 z = 3 - t
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x - y - z - 1 0 và cho đường thẳng
d
:
x
+
1
2
y
-
1
1
z
-
2
3
, cho A(1; 1; -2). Viết phương trình đường thẳng đi qua A, song song với (P) và vuông g...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x - y - z - 1 = 0 và cho đường thẳng d : x + 1 2 = y - 1 1 = z - 2 3 , cho A(1; 1; -2). Viết phương trình đường thẳng đi qua A, song song với (P) và vuông góc với d
A. x - 1 2 = y - 1 5 = z + 2 3
B. x - 1 2 = y - 1 - 5 = z 2
C. x - 1 2 = y - 1 - 5 = z + 2 - 3
D. x - 1 2 = y - 1 5 = z + 2 - 3
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
a
:
x
1
y
1
z
-
2
;
b
:
x
+
1
-
2
y
2
z...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng a : x 1 = y 1 = z - 2 ; b : x + 1 - 2 = y 2 = z + 1 - 1 và mặt phẳng ( P ) : x - y - z = 0 . Viết phương trình của đường thẳng d song song với (P), cắt a và b lần lượt tại M và N mà M N = 2 .
A. d : 7 x - 4 3 = 7 y + 4 8 = 7 z + 8 - 5
B. d : 7 x + 4 3 = 7 y - 4 8 = 7 z + 8 - 5 .
C. d : 7 x - 1 3 = 7 y - 4 8 = 7 z + 3 - 5
D. d : 7 x - 1 3 = 7 y + 4 8 = 7 z + 8 - 5
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
P
:
x
-
y
-
z
-
1
0
và cho đường thẳng
d
:
x
+
1
2
y
-
1
1
z
-
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : x - y - z - 1 = 0 và cho đường thẳng d : x + 1 2 = y - 1 1 = z - 2 3 , cho A 1 ; 1 ; - 2 Đường thẳng đi qua A, song song với (P) và vuông góc với d có phương trình là
A. x - 1 2 = y - 1 5 = z + 2 3
B. x - 1 2 = y - 1 - 5 = z 2
C. x - 1 2 = y - 1 - 5 = z + 2 3
D. x - 1 2 = y - 1 5 = z + 2 - 3
Trong không gian với hệ tọa độ (Oxyz), cho đường thẳng
d
:
x
1
y
-
1
2
z
+
1
1
và mặt phẳng (P): x + y + z - 2 0. Gọi d là đường thẳng vuông góc d và song song với mp(P). Véctơ chỉ phương của d là: A.
u
→...
Đọc tiếp
Trong không gian với hệ tọa độ (Oxyz), cho đường thẳng d : x 1 = y - 1 2 = z + 1 1 và mặt phẳng (P): x + y + z - 2 = 0. Gọi d' là đường thẳng vuông góc d và song song với mp(P). Véctơ chỉ phương của d' là:
A. u → = 0 ; - 1 ; 1
B. u → = 1 ; 0 ; - 1
C. u → = 2 ; - 1 ; - 1
D. u → = 1 ; 1 ; - 2
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng
d
:
x
-
1
1
y
-
1
2
z
-
2
-
3
và cho mặt phẳng (P): x + y + z -4 0. Khẳng định nào dưới đây là khẳng định...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng d : x - 1 1 = y - 1 2 = z - 2 - 3 và cho mặt phẳng (P): x + y + z -4 = 0. Khẳng định nào dưới đây là khẳng định đúng?
A. d c ắ t ( P )
B. d / / ( P )
C. d ⊂ ( P )
D. d ⊥ ( P )
Trong không gian với hệ tọa độ Oxyz cho điểm A(1;-1;1), mặt phẳng (P): x–2y+z-10 và đường thẳng d:
x
1
y
-
2
2
z
+
1
-
1
. Viết phương trình đường thẳng đi qua A, song song với mặt phẳng (P) cắt đường thẳng d. A.
x...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho điểm A(1;-1;1), mặt phẳng (P): x–2y+z-1=0 và đường thẳng d: x 1 = y - 2 2 = z + 1 - 1 . Viết phương trình đường thẳng đi qua A, song song với mặt phẳng (P) cắt đường thẳng d.
A. x - 1 1 = y + 1 1 = z - 1 1
B. x - 1 15 = y + 1 7 = z - 1 1
C. x - 1 4 = y + 1 1 = z - 1 - 2
D. x - 1 13 = y + 1 6 = z - 1 - 1
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
P
x
+
y
+
z
−
3
0
và đường thẳng
d
:
x
1
y
+
1
2
z
−
2
−...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P = x + y + z − 3 = 0 và đường thẳng d : x 1 = y + 1 2 = z − 2 − 1 . Đường thẳng d ' đối xứng với d qua mặt phẳng (P) có phương trình là
A. x + 1 1 = y + 1 2 = z + 1 7
B. x + 1 1 = y + 1 − 2 = z + 1 7
C. x − 1 1 = y − 1 2 = z − 1 7
D. x − 1 1 = y − 1 − 2 = z − 1 7
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P): x+y+z-20, (Q): x+2y-z+30 và điểm A(1;0;4). Phương trình đường thẳng qua A và cùng song song với (P) và (Q) là: A.
d
:
x
-
1
-
3
y
2
...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P): x+y+z-2=0, (Q): x+2y-z+3=0 và điểm A(1;0;4). Phương trình đường thẳng qua A và cùng song song với (P) và (Q) là:
A. d : x - 1 - 3 = y 2 = z - 4 1
B. d : x - 1 3 = y 1 = z - 4 1
C. d : x - 1 - 3 = y - 1 = z - 4 1
D. d : x - 1 - 3 = y 2 = z - 4 - 1
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
∆
đi qua điểm
M
1
;
1
;
−
2
song song với mặt phẳng
P
:
x
−
y
−
z
−
1
0
và cắt đường
d
:
x
+
1...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ∆ đi qua điểm M 1 ; 1 ; − 2 song song với mặt phẳng P : x − y − z − 1 = 0 và cắt đường
d : x + 1 − 2 = y − 1 1 = z − 1 3 , thẳng phương trình của ∆ là:
A. x + 1 2 = y + 1 5 = z − 2 − 3
B. x − 1 2 = y − 1 5 = z + 2 − 3
C. x + 5 − 2 = y + 3 1 = z − 1
D. x + 1 − 2 = y + 1 5 = z − 2 3