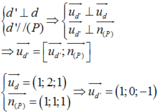Các câu hỏi tương tự
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x - y - z - 1 0 và cho đường thẳng
d
:
x
+
1
2
y
-
1
1
z
-
2
3
, cho A(1; 1; -2). Viết phương trình đường thẳng đi qua A, song song với (P) và vuông g...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x - y - z - 1 = 0 và cho đường thẳng d : x + 1 2 = y - 1 1 = z - 2 3 , cho A(1; 1; -2). Viết phương trình đường thẳng đi qua A, song song với (P) và vuông góc với d
A. x - 1 2 = y - 1 5 = z + 2 3
B. x - 1 2 = y - 1 - 5 = z 2
C. x - 1 2 = y - 1 - 5 = z + 2 - 3
D. x - 1 2 = y - 1 5 = z + 2 - 3
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d:
x
1
y
-
1
2
z
+
2
2
mặt phẳng (P): 2x+y+2z-50 và điểm A(1; 1; -2) Phương trình chính tắc của đường thẳng
∆
đi qua A song song với mặt phẳng (P) và vuông góc với d là A.
∆
:...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: x 1 = y - 1 2 = z + 2 2 mặt phẳng (P): 2x+y+2z-5=0 và điểm A(1; 1; -2) Phương trình chính tắc của đường thẳng ∆ đi qua A song song với mặt phẳng (P) và vuông góc với d là
A. ∆ : x - 1 1 = y - 1 2 = z + 2 - 2
B. ∆ : x - 1 2 = y - 1 1 = z + 2 - 2
C. ∆ : x - 1 2 = y - 1 2 = z + 2 - 3
D. ∆ : x - 1 1 = y - 2 2 = z + 2 2
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
P
:
x
-
y
-
z
-
1
0
và cho đường thẳng
d
:
x
+
1
2
y
-
1
1
z
-
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P : x - y - z - 1 = 0 và cho đường thẳng d : x + 1 2 = y - 1 1 = z - 2 3 , cho A 1 ; 1 ; - 2 Đường thẳng đi qua A, song song với (P) và vuông góc với d có phương trình là
A. x - 1 2 = y - 1 5 = z + 2 3
B. x - 1 2 = y - 1 - 5 = z 2
C. x - 1 2 = y - 1 - 5 = z + 2 3
D. x - 1 2 = y - 1 5 = z + 2 - 3
Trong không gian với hệ tọa độ Oxyz cho mặt phẳng
P
:
x
+
y
-
4
z
0
đường thẳng d:
x
-
1
2
y
+
1
-
1
z
-
3...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho mặt phẳng P : x + y - 4 z = 0 đường thẳng d: x - 1 2 = y + 1 - 1 = z - 3 1 và điểm A 1 ; 3 ; 1 thuộc mặt phẳng (P). Gọi ∆ là đường thẳng đi qua A nằm trong mặt phẳng (P) và cách d một khoảng cách lớn nhất. Gọi u → = 1 ; b ; c là một vectơ chỉ phương của đường thẳng ∆ . Tính b + c
A. b + c = - 6 11
B. b + c = 0
C. b + c = 1 4
D. b + c = 4.
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
∆
:
x
-
2
1
y
-
2
1
z
-
1
2
và mặt phẳng (α):x+y+z-10. Gọi d là đường thẳng nằm trên (α) đồng thời cắt đường thẳng ∆ và trục Oz. Một véctơ chỉ phương của...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ∆ : x - 2 1 = y - 2 1 = z - 1 2 và mặt phẳng (α):x+y+z-1=0. Gọi d là đường thẳng nằm trên (α) đồng thời cắt đường thẳng ∆ và trục Oz. Một véctơ chỉ phương của d là:
A. u → = 1 ; - 2 ; 1
B. u → = 1 ; 1 ; - 2
C. u → = 2 ; - 1 ; - 1
D. u → = 1 ; 2 ; - 3
Trong không gian với hệ toạ độ Oxyz, cho đường thẳng
∆
là giao tuyến của hai mặt phẳng
P
:
z
-
1
0
và
Q
:
x
+
y
+
z
-
3
0
. Gọi d là đường thẳng nằm trong mặt phẳng
P
, cắt đường thẳng...
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho đường thẳng ∆ là giao tuyến của hai mặt phẳng P : z - 1 = 0 và Q : x + y + z - 3 = 0 . Gọi d là đường thẳng nằm trong mặt phẳng P , cắt đường thẳng x - 1 1 = y - 2 - 1 = z - 3 - 1 và vuông góc với đường thẳng . Phương trình của đường thẳng d là
A. x = 3 + t y = t z = 1 + t
B. x = 3 - t y = t z = 1
C. x = 3 + t y = t z = 1
D. x = 3 + t y = - t z = 1 + t
Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng
(
α
)
:x+y-z+10 và đường thẳng d:
x
-
1
1
y
-
2
2
z
-
3
3
. Đường thẳng
Δ
qua điểm A(1;0;2) và có véctơ chỉ phương...
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng ( α ) :x+y-z+1=0 và đường thẳng d: x - 1 1 = y - 2 2 = z - 3 3 . Đường thẳng Δ qua điểm A(1;0;2) và có véctơ chỉ phương u → (a;b;1), cách đường thẳng d một khoảng bằng
A. 3 3
B. 3
C. 2 2
D. 2
Trong không gian với hệ tọa độ Oxyz cho điểm A(1;-1;1), mặt phẳng (P): x–2y+z-10 và đường thẳng d:
x
1
y
-
2
2
z
+
1
-
1
. Viết phương trình đường thẳng đi qua A, song song với mặt phẳng (P) cắt đường thẳng d. A.
x...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho điểm A(1;-1;1), mặt phẳng (P): x–2y+z-1=0 và đường thẳng d: x 1 = y - 2 2 = z + 1 - 1 . Viết phương trình đường thẳng đi qua A, song song với mặt phẳng (P) cắt đường thẳng d.
A. x - 1 1 = y + 1 1 = z - 1 1
B. x - 1 15 = y + 1 7 = z - 1 1
C. x - 1 4 = y + 1 1 = z - 1 - 2
D. x - 1 13 = y + 1 6 = z - 1 - 1
Trong không gian với hệ tọa độ oxyz, cho mặt phẳng
P
:
x
+
y
+
z
-
3
0
và đường thẳng
d
:
x
-
2
1
y
+
1
-
2
z...
Đọc tiếp
Trong không gian với hệ tọa độ oxyz, cho mặt phẳng P : x + y + z - 3 = 0 và đường thẳng d : x - 2 1 = y + 1 - 2 = z - 1 . Gọi I là giao điểm của mặt phẳng (P) với đường thẳng d. Điểm M thuộc mặt phẳng (P) có hoành độ dương sao cho IM vuông góc với d và I M = 4 14 có tọa độ là:
A. M(5;9;-11)
B. M(-3;-7;13)
C. M(5;9;11)
D. M(3;-7;13)