Đáp án A
Mặt phẳng qua I vuông góc với d có phương trình
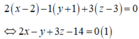
Gọi H là hình chiếu của I trên đường thẳng d.
Thay x, y, z từ phương trình của d vào ta có

Đáp án A
Mặt phẳng qua I vuông góc với d có phương trình
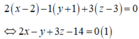
Gọi H là hình chiếu của I trên đường thẳng d.
Thay x, y, z từ phương trình của d vào ta có

Trong không gian với hệ tọa độ Oxyz , cho đường thẳng d có phương trình lần lượt d : x = 1 + 2 t , y = 2 − t , z = 3 t . Tìm tọa độ điểm K đối xứng với điểm I 2 ; − 1 ; 3 qua đường thẳng d.
A. K − 4 ; − 3 ; − 3
B. K − 1 ; 3 ; − 3
C. K 4 ; 3 ; 3
D. K 1 ; − 3 ; 3
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x + 2 2 = y - 4 - 3 = z + 1 1 và điểm M ( 2;-1;3 ) . Viết phương trình mặt phẳng (P) đi qua điểm K ( 1;0;0 ), song song với đường thẳng d đồng thời cách điểm M một khoảng bằng 3
A. (P): 17x + 5y - 19z + 17 = 0
B. (P): 17x + 5y - 19z - 17 = 0
C. (P): 17x - 5y - 19z + 17 = 0
D. (P): 17x - 5y - 19z - 17 = 0
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng P = x + y + z − 3 = 0 và đường thẳng d : x 1 = y + 1 2 = z − 2 − 1 . Đường thẳng d ' đối xứng với d qua mặt phẳng (P) có phương trình là
A. x + 1 1 = y + 1 2 = z + 1 7
B. x + 1 1 = y + 1 − 2 = z + 1 7
C. x − 1 1 = y − 1 2 = z − 1 7
D. x − 1 1 = y − 1 − 2 = z − 1 7
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d 1 v à d 2 lần lượt có phương trình là x − 1 1 = y − 2 3 = z − 3 − 1 , x − 2 − 2 = y + 2 1 = z − 1 3 . Tìm tọa độ giao điểm M của d 1 và d.
A. M = (0;–1;4)
B. M = (0;1;4)
C. M = (–3;2;0)
D. M = (3;0;5)
Trong không gian với hệ tọa độ Oxyz, cho điểm A 1 ; 2 ; 2 và đường thẳng d : x - 6 2 = y - 1 1 = z - 5 1 . Tìm tọa độ điểm B đối xứng với A qua d.
A. B (-3; 4; -4).
B. B (2; -1; 3)
C. B (3; 4; -4)
D. B (3; -4; 4) .
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng x = 1 + t y = 2 − t z = t , d ' : x = 2 t ' y = 1 + t ' z = 2 + t ' . Đường thẳng ∆ cắt d , d ' lần lượt tại các điểm A, B thỏa mãn độ dài đoạn thẳng AB nhỏ nhất. Phương trình đường thẳng ∆ là
A. x − 1 − 2 = y − 2 1 = z 3 .
B. x − 4 − 2 = y − 1 = z − 2 3 .
C. x 2 = y − 3 − 1 = z + 1 − 3 .
D. x − 2 − 2 = y − 1 1 = z − 1 3 .
Trong không gian với hệ tọa độ Oxyz, cho điểm M(3;3;-2) và hai đường thẳng d 1 : x - 1 1 = y - 2 3 = z 1 ; d 2 : x + 1 - 1 = y - 1 2 = z - 2 4 . Đường thẳng d qua M cắt d1; d2 lần lượt tại A và B. Độ dài đoạn thẳng AB bằng
A. 3
B. 2
C. 6
D. 5
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P) và đường thẳng d tương ứng có phương trình là 2 x - y + 3 z - 3 = 0 và x + 1 - 2 = y - 2 1 = z + 2 - 1 . Biết đường thẳng d cắt mặt phẳng (P) tại điểm M. Gọi N là điểm thuộc d sao cho M N = 3 , gọi K là hình chiếu vuông góc của điểm N trên mặt phẳng (P). Tính độ dài đoạn MK.
A. M K = 7 105
B. M K = 7 4 21
C. M K = 4 21 7
D. M K = 105 7
Trong không gian với hệ tọa độ Oxyz cho điểm M(3;3;-2) và hai đường thẳng d 1 : x - 1 1 = y - 2 3 = z 1 , d 2 : x + 1 - 1 = y - 1 2 = z - 2 4 . Đường thẳng d đi qua M cắt d 1 , d 2 lần lượt tại A và B. Tính độ dài đoạn thẳng AB ?
A. AB = 2
B. AB = 3
C. AB = 6
D. AB = 5