Đáp án A
Gọi 
Ta có:
M
A
→
=
k
M
B
→
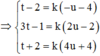
Giả hệ với ẩn t; k và ku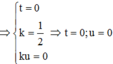 
Trong không gian với hệ tọa độ Oxyz cho điểm M(3;3;-2) và hai đường thẳng d 1 : x - 1 1 = y - 2 3 = z 1 , d 2 : x + 1 - 1 = y - 1 2 = z - 2 4 . Đường thẳng d đi qua M cắt d 1 , d 2 lần lượt tại A và B. Tính độ dài đoạn thẳng AB ?
A. AB = 2
B. AB = 3
C. AB = 6
D. AB = 5
Trong không gian Oxyz, cho điểm M(3;3;-2) và 2 đường thẳng d 1 : x - 1 1 = y - 2 3 = z 1 , d 2 : x + 1 - 1 = y - 1 2 = z - 2 4 . Đường thẳng đi qua M và cắt cả 2 đường thẳng d 1 , d 2 tại A, B. Độ dài đoạn thẳng AB bằng
A. 2 2
B. 6
C. 3
D. 2
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;-1;3) và hai đường thẳng, d 1 : x - 4 1 = y + 2 4 = z - 1 - 2 , d 2 = x - 2 1 = y + 1 - 1 = z - 1 1 . Viết phương trình đường thẳng d đi qua A, vuông góc với đường thẳng d 1 và cắt đường thẳng d 2 .
A. d : x - 4 4 = y + 1 1 = z - 3 4
B. d : x - 1 2 = y + 1 1 = z - 3 3
C. d : x - 1 2 = y + 1 - 1 = z - 3 - 1
D. d : x - 1 - 2 = y + 1 2 = z - 3 3
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d 1 : x - 1 1 = y - 1 1 = z + 1 1 và d 2 : x + 1 2 = y - 1 - 1 = z 2 . Đường thẳng qua điểm M(1;1;1) và cắt d 1 , d 2 lần lượt tại A, B. Tính tỉ số MA/MB.
A. M A M B = 3 2 .
B. M A M B = 2.
C. M A M B = 1 2 .
D. M A M B = 2 3 .
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d 1 v à d 2 lần lượt có phương trình là x − 1 1 = y − 2 3 = z − 3 − 1 , x − 2 − 2 = y + 2 1 = z − 1 3 . Tìm tọa độ giao điểm M của d 1 và d.
A. M = (0;–1;4)
B. M = (0;1;4)
C. M = (–3;2;0)
D. M = (3;0;5)
Trong không gian với hệ tọa độ Oxyz cho ba đường thẳng d 1 : x = t y = 4 − t z = − 1 + 2 t , d 2 : x 1 = y − 2 − 3 = z − 3 v à d 3 : x + 1 5 = y − 1 2 = z + 1 1 . Gọi ∆ là đường thẳng cắt d 1 , d 2 , d 3 lần lượt tại các điểm A, B, C sao cho AB = BC. Phương trình đường thẳng ∆ là
A. x − 2 1 = y − 2 1 = z 1
B. x 1 = y − 2 1 = z 1
C. x 1 = y − 3 1 = z − 1 − 1
D. x 1 = y − 3 − 1 = z − 1 1
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d 1 = x - 1 1 = y - 1 1 = z + 1 1 và d 2 = x + 1 2 = y - 1 - 1 = z 2 Đường thẳng qua điểm M 1 ; 1 ; 1 và cắt d1, d2 lần lượt tại A, B. Tính tỉ số M A M B
A. M A M B = 3 2 .
B. M A M B = 2 .
C. M A M B = 1 2 .
D. M A M B = 2 3 .
Trong không gian với hệ tọa độ Oxyz, cho điểm A (1;2;1) và hai đường thẳng d 1 : x - 1 1 = y + 1 1 = z - 3 - 1 ; d 2 : x - 1 1 = y + 2 1 = z - 2 1 . Viết phương trình đường thẳng d song song với mặt phẳng P : 2 x + 3 y + 4 z - 6 = 0 , cắt đường thẳng d 1 , d 2 lần lượt tại M và N sao cho A M → A N → = 5 và điểm N có hoành độ nguyên.
A. d : x - 2 1 = y - 2 = z - 2 1
B. d : x - 3 1 = y - 1 2 = z - 1 - 2
C. d : x 3 = y + 2 2 = z - 4 - 3
D. d : x - 1 4 = y + 1 - 4 = z - 3 1
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d 1 : x - 1 1 = y - 1 2 = z - 1 1 ; d 2 : x 1 = y + 1 2 = z - 6 - 5 . gọi A là giao điểm của d 1 v à d 2 ; d là đường thẳng qua điểm M (2; 3;1) cắt d 1 , d 2 lần lượt tại B, C sao cho B C = 6 A B . Tính khoảng cách từ O đến đường thẳng d, biết rằng d không song song với mặt phẳng (Oxz)
A. 10 5
B. 10 3
C. 13
D. 10
