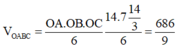
Đáp án B
Gọi H là hình chiếu của O trên (P)
Dấu bằng xảy ra khi và chỉ khi
Mặt phẳng (P) cắt các trục tọa độ lần lượt tại
Vậy thể tích khối chóp OABC là
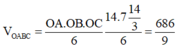
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;2;3). Gọi (P) là mặt phẳng đi qua điểm M và cách gốc tọa độ O một khoảng lớn nhất, mặt phẳng (P) cắt các trục tọa độ tại các điểm A, B, C. Tính thể tích khối chóp O.ABC
A. 1372/9
B. 686/9
C. 524/3
D. 343/9
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;2;3). Gọi (P) là mặt phẳng đi qua điểm Mvà cách gốc tọa độ O một khoảng lớn nhất, mặt phẳng (P) cắt các trục tọa độ tại các điểm A,B,C. Tính thể tích khối chóp O.ABC.
A. 1372 9
B. 686 9
C. 524 3
D. 343 9
Trong không gian với hệ tọa độ Oxy, cho mặt phẳng (P): 2y-z+3=0 và điểm A (2;0;0). Mặt phẳng (α) đi qua A, vuông góc với (P), cách gốc tọa độ O một khoảng bằng 4/3 và cắt các tia Oy, Oz lần lượt tại các điểm B, C khác O. Thể tích khối tứ diện OABC bằng:
A. 8.
B. 16
C. 8/3
D. 16/3
Trong không gian với hệ tọa độ Oxyz, cho điểm M(3;2;1). Mặt phẳng (P) đi qua M và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với gốc tọa độ sao cho M là trực tâm tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P).
A. 3x+2y+z+14=0
B. 2x+y+3z+9=0
C. 3x+2y+z-14=0
D. 2x+y+z-9=0.
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(1;2;5). Số mặt phẳng đi qua M và cắt các trục Ox, Oy, Oz tại A, B, C sao cho OA = OB = OC (A, B, C không trùng với gốc tọa độ O) là:
A. 8
B. 3
C. 4
D. 1
Trong không gian với hệ tọa độ Oxyz. Viết phương trình mặt phẳng (P) đi qua điểm M(1;2;3) và cắt trục Ox, Oy, Oz lần lượt tại ba điểm A, B, C khác với gốc tọa độ O sao cho biểu thức 1 O A 2 + 1 O B 2 + 1 O C 2 có đạt giá trị nhỏ nhất
A. P : x + 2 y + 3 z − 14 = 0
B. P : x + 2 y + 3 z − 11 = 0
C. P : x - y - 3 z − 14 = 0
D. P : x + y + 3 z − 14 = 0
Trong không gian với hệ tọa độ Oxyz, cho điểm M(4;1;9). Gọi (P) là mặt phẳng đi qua M và cắt 3 tia Ox, Oy, Oz lần lượt tại các điểm A,B,C (khác 0) sao cho (OA+OB+OC) đạt giá trị nhỏ nhất. Tính khoảng cách d từ điểm I(0;1;3) đến mặt phẳng (P).
A. d= 34 5
B. d= 36 5
C. d= 24 7
D. d= 30 7
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm M(1;2;3) và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O). Viết phương trình mặt phẳng (P) sao cho M là trực tâm của tam giác ABC.
A. 6x +3y-2z -6=0
B. x +2y+3z -14=0
C. x +2y+3z -11=0
D. x 1 + y 2 + z 3 = 3
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;2;1). Mặt phẳng (P) thay đổi đi qua M cắt các tia Ox, Oy, Oz lần lượt tại A, B, C khác gốc tọa độ. Tính giá trị nhỏ nhất của thể tích khối tứ diện OABC
A. 18
B. 9
C. 6
D. 54
