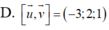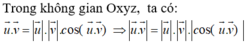Các câu hỏi tương tự
Trong không gian Oxyz, cho hai vectơ
u
→
(x; y; z),
v
→
(x; y; z). Khẳng định nào dưới đây sai? A.
u
→
x
2
+
y
2
+
z
2
B...
Đọc tiếp
Trong không gian Oxyz, cho hai vectơ u → = (x; y; z), v → = (x'; y'; z'). Khẳng định nào dưới đây sai?
A. u → = x 2 + y 2 + z 2
B. u → + v → = x + x ' ; y + y ' ; z + z '
C. u → . v → = x + y + z . x ' + y ' + z '
D. u → ⊥ v → ⇔ x . x ' + y . y ' + z . z ' = 0
Trong không gian Oxyz, cho hai vectơ
u
→
(x; y; z),
v
→
(x; y; z) khác
0
→
. Khẳng định nào dưới đây sai? A.
u
→
2
x
2
+
y
2
+
z
2...
Đọc tiếp
Trong không gian Oxyz, cho hai vectơ u → = (x; y; z), v → = (x'; y'; z') khác 0 → . Khẳng định nào dưới đây sai?
A. u → 2 = x 2 + y 2 + z 2 c
B. u → 2 = u → . v → ⇔ u → = v →
C. u → - v → = x - x ' ; y - y ' ; z - z '
D. cos u → ; v → = u → . v → u → . v →
Trong không gian với hệ tọa độ Oxyz ,cho hai vectơ
u
→
(
1
;
2
;
3
)
và
v
→
(
-
5
;
1
;
1
)
. Khẳng định nào đúng? A. ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz ,cho hai vectơ u → = ( 1 ; 2 ; 3 ) và v → = ( - 5 ; 1 ; 1 ) . Khẳng định nào đúng?
A. u → = v →
B. u → ⊥ v →
C. u → = v →
D. u → / / v →
Trong không gian với hệ tọa độ Oxyz, cho hai vectơ
u
→
1
;
2
;
3
v
à
v
→
-
5
;
1
;
1
. Khẳng định nào đúng? A.
u
→
v
→
B....
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai vectơ u → = 1 ; 2 ; 3 v à v → = - 5 ; 1 ; 1 . Khẳng định nào đúng?
A. u → = v →
B. u → ⊥ v →
C. u → = v →
D. u → / / v →
Trong không gian Oxyz, véc tơ nào dưới đây vuông góc với cả hai véc tơ
u
→
(
-
1
;
0
;
2
)
,
v
→
(
4
;
0...
Đọc tiếp
Trong không gian Oxyz, véc tơ nào dưới đây vuông góc với cả hai véc tơ u → = ( - 1 ; 0 ; 2 ) , v → = ( 4 ; 0 ; - 1 ) ?
A. w → =(0;7;1)
B. w → =(1;7;1)
C. w → =(0;-1;0)
D. w → =(-1;7-1)
Trong không gian với hệ tọa độ Oxyz, biết
u
→
2
;
v
→
1
; và góc giữa hai vectơ
u
→
và
v
→
bằng
2
π
3
. Tìm k để vectơ
p
→
k
u
→
+
v
→
vuôn...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, biết u → = 2 ; v → = 1 ; và góc giữa hai vectơ u → và v → bằng 2 π 3 . Tìm k để vectơ p → = k u → + v → vuông góc với vectơ q → = u → - v → .
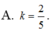
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho vectơ
u
→
(
3
;
0
;
1
)
và
v
→
(
2
;
0
;
1
)
. Tính tích vô hướng
u
→
.
v
→
.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho vectơ u → = ( 3 ; 0 ; 1 ) và v → = ( 2 ; 0 ; 1 ) . Tính tích vô hướng u → . v → .
![]()
![]()
![]()
![]()
Cho số phức u và v. Xét các mệnh đề dưới đây1.
u
+
v
u
+
v
2.
u
−
v
u
−
v
3.
u
.
v
u
.
v
4. ...
Đọc tiếp
Cho số phức u và v. Xét các mệnh đề dưới đây
1. u + v = u + v
2. u − v = u − v
3. u . v = u . v
4. u v = u v v ≠ 0
Hỏi có bao nhiêu mệnh đề đúng trong 4 mệnh đề trên?
A. 1
B. 2
C. 3
D. 4
Trong không gian hệ tọa độ Oxyz, cho
u
→
(
1
;
2
;
-
1
)
và
v
→
(
2
;
1
;
0
)
. Tính
[
u
→
,
v
→
]
.
Đọc tiếp
Trong không gian hệ tọa độ Oxyz, cho u → = ( 1 ; 2 ; - 1 ) và v → = ( 2 ; 1 ; 0 ) . Tính [ u → , v → ] .
![]()
![]()
![]()