Các câu hỏi tương tự
Trong không gian với hệ tọa độ Oxyz, cho hai vectơ
u
→
1
;
2
;
3
v
à
v
→
-
5
;
1
;
1
. Khẳng định nào đúng? A.
u
→
v
→
B....
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai vectơ u → = 1 ; 2 ; 3 v à v → = - 5 ; 1 ; 1 . Khẳng định nào đúng?
A. u → = v →
B. u → ⊥ v →
C. u → = v →
D. u → / / v →
Trong không gian với hệ tọa độ Oxyz, biết
u
→
2
;
v
→
1
; và góc giữa hai vectơ
u
→
và
v
→
bằng
2
π
3
. Tìm k để vectơ
p
→
k
u
→
+
v
→
vuôn...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, biết u → = 2 ; v → = 1 ; và góc giữa hai vectơ u → và v → bằng 2 π 3 . Tìm k để vectơ p → = k u → + v → vuông góc với vectơ q → = u → - v → .
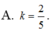
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho vectơ
u
→
(
3
;
0
;
1
)
và
v
→
(
2
;
0
;
1
)
. Tính tích vô hướng
u
→
.
v
→
.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho vectơ u → = ( 3 ; 0 ; 1 ) và v → = ( 2 ; 0 ; 1 ) . Tính tích vô hướng u → . v → .
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho hai véctơ
u
→
2
;
3
;
-
1
và
v
→
5
;
-
4
;
m
. Tìm m để
u
→...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai véctơ u → = 2 ; 3 ; - 1 và v → = 5 ; - 4 ; m . Tìm m để u → ⊥ v →
A. - 2
B. 2
C. 4
D. 0
Trong không gian Oxyz, cho hai vectơ
u
→
(-1; 3; 4),
v
→
(2; -1; 5). Tích có hướng của hai vectơ
u
→
và
v
→
là: A.
u
→
,
v
→...
Đọc tiếp
Trong không gian Oxyz, cho hai vectơ u → = (-1; 3; 4), v → = (2; -1; 5). Tích có hướng của hai vectơ u → và v → là:
A. u → , v → = 19 ; 13 ; - 5
B. u → , v → = 19 ; - 13 ; - 5
C. u → , v → = - 19 ; 13 ; - 5
D. u → , v → = 19 ; 13 ; 5
Trong không gian với hệ tọa độ Oxyz, cho các vectơ
a
→
1
;
1
;
0
,
b
→
2
;
-
1
;
-
2
,
c
→
-
3
;
0...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho các vectơ a → = 1 ; 1 ; 0 , b → = 2 ; - 1 ; - 2 , c → = - 3 ; 0 ; 2 . Khẳng định nào đúng?
A. a → b → + c → = 0
B. 2 a → + b → = c →
C. a → = 2 b → - c →
D. a → + b + c → = 0
Trong không gian hệ tọa độ Oxyz, cho
u
→
(
1
;
2
;
-
1
)
và
v
→
(
2
;
1
;
0
)
. Tính
[
u
→
,
v
→
]
.
Đọc tiếp
Trong không gian hệ tọa độ Oxyz, cho u → = ( 1 ; 2 ; - 1 ) và v → = ( 2 ; 1 ; 0 ) . Tính [ u → , v → ] .
![]()
![]()
![]()
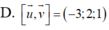
Trong không gian Oxyz, cho hai vectơ
u
→
(3; 4; 0),
v
→
(2; -1; 2) . Tích vô hướng của hai vectơ
u
→
và
v
→
là: A. 15 B. 2 C. 3 D. 0
Đọc tiếp
Trong không gian Oxyz, cho hai vectơ u → = (3; 4; 0), v → = (2; -1; 2) . Tích vô hướng của hai vectơ u → và v → là:
A. 15
B. 2
C. 3
D. 0
Trong không gian với hệ tọa độ Oxyz, cho vecto
u
→
(
x
;
2
;
1
)
và vec tơ
v
→
(
1
;
-
1
;
2
x
)
. Tính...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho vecto u → = ( x ; 2 ; 1 ) và vec tơ v → = ( 1 ; - 1 ; 2 x ) . Tính tích vô hướng của u → v à v → .
A. -2 - x
B. 3x + 2
C. 3x - 2
D. x + 2



