Chọn D

Tức là tứ diện SABC có các cạnh SA, SB, SC bằng nhau và đôi một vuông góc.
Vậy tứ diện SABC có tất cả ba mặt phẳng đối xứng đó là:
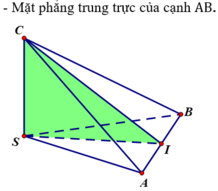
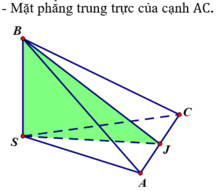
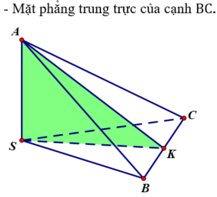
Chọn D

Tức là tứ diện SABC có các cạnh SA, SB, SC bằng nhau và đôi một vuông góc.
Vậy tứ diện SABC có tất cả ba mặt phẳng đối xứng đó là:



Trong không gian với hệ tọa độ Oxyz, cho A ( 1 ; 0 ; 2 ) , B ( 3 ; 1 ; 4 ) , C ( 3 ; - 2 ; 1 ) . Tìm tọa độ điểm S, biết SA vuông góc với (ABC), mặt cầu ngoại tiếp tứ diện S.ABC có bán kính bằng 3 11 2 và S có cao độ âm
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho A(1;0;2), B(3;1;4), C(3;-2;1). Tìm tọa độ điểm S, biết SA vuông góc với (ABC), mặt cầu ngoại tiếp tứ diện S.ABC có bán kính bằng 3 11 2 và S có cao độ âm.
A. S(4;6;-4)
B.S(4;-6;-4)
C. S(-4;6;-4)
D. S(-4;-6;-4)
Trong không gian Oxxyz, cho điểm A(1;0;0), B(0;-1;0), C(0;0;1), D(1;-1;1) . Mặt cầu tiếp xúc 6 cạnh của tứ diện ABCD cắt (ACD) theo thiết diện có diện tích S. Chọn mệnh đề đúng?
A. S = π 3
B. S = π 6
C. S = π 4
D. S = π 5
Trong không gian Oxyz cho A(-1;0;0), B(0;0;2), C(0;-3;0). Tính bán kính mặt cầu ngaoij tiếp tứ diện OABC
A. 14 3
B . 14 4
C. 14 2
D. 14
Trong không gian với hệ trục tọa độ Oxyz cho A(-1;0;0), B(0;0;2), C(0;-3;0). Bán kính mặt cầu ngoại tiếp tứ diện OABC là
A. 14 3
B. 14 4
C. 14 2
D. 14
Trong không gian Oxyz, cho hai điểm A (1;0;0), B (0;0;2) và mặt cầu (S): x²+y²+z²-2x-2y+1=0. Hỏi có tất cả bao nhiêu mặt phẳng chứa hai điểm A, B và tiếp xúc với (S).
A.3.
B. 0
C. 1
D. 2
Trong không gian với hệ tọa độ Oxyz cho điểm A(2;0;0), B(0;2;0), C(0;0;2), D(2;2;2). Tính bán kính mặt cầu ngoại tiếp khối tứ diện ABCD.
A. 2 .
B. 2 2 .
C. 3 .
D. 2 3 .
Trong không gian Oxyz, cho tam giác ABC có diện tích bằng 6 nằm trên mặt phẳng (P):x-2y+z+2=0 và điểm S(1;2;-1). Tính thể tích V của khối chóp S.ABC
![]()
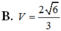
![]()
![]()
Trong không gian Oxyz, cho ba điểm A (3; 0; 0), B (1; 2; 1) và C (2; -1; 2). Biết mặt phẳng qua B, C và tâm mặt cầu nội tiếp tứ diện OABC có một vectơ pháp tuyến là (10; a; b). Tổng a + b là:
A. -2
B. 2
C. 1
D. -1