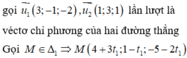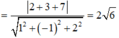Các câu hỏi tương tự
Trong không gian Oxyz, cho hai đường thẳng
△
1
:
x
-
4
3
y
-
1
-
1
z
+
5
-
2...
Đọc tiếp
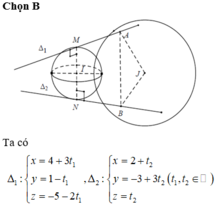
Trong không gian Oxyz, cho hai đường thẳng △ 1 : x - 4 3 = y - 1 - 1 = z + 5 - 2 và △ 2 : x - 2 = y + 3 = z 1 Trong tất cả các mặt cầu tiếp xúc với cả hai đường thẳng △ 1 và △ 2 Gọi (S) là mặt cầu có bán kính nhỏ nhất. Bán kính của mặt cầu (S) là
A. 12
B. 6
C. 24
D. 3
Trong không gian Oxyz cho hai đường thẳng
∆
1
:
x
1
y
2
+
t
z
-
t
,
∆
2
:...
Đọc tiếp
Trong không gian Oxyz cho hai đường thẳng ∆ 1 : x = 1 y = 2 + t z = - t , ∆ 2 : x = 4 + t y = 3 - 2 t z = 1 - t .Gọi (S) là mặt cầu có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng Δ1 và Δ2. Bán kính mặt cầu (S).
A . 10 2
B . 11 2
C. 3/2
D. 2
Trong không gian Oxyz, cho mặt cầu (S):
(
x
+
1
)
2
+
(
y
-
1
)
2
+
(
z
+
2
)
2
3
và hai đường thẳn...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): ( x + 1 ) 2 + ( y - 1 ) 2 + ( z + 2 ) 2 = 3 và hai đường thẳng d x : x - 2 1 = y 2 = z - 1 - 1 ; △ : x 1 = y 1 = z - 1 - 1 Phương trình nào dưới đây là phương trình mặt phẳng cắt mặt cầu (S) theo giao tuyến là một đường tròn (C) có bán kính bằng 1 và song song với d và △ .
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho mặt cầu (S): (x-1)²+ (y-2)²+ (z-3)²25 và hai điểm A (3;-2;6), B (0;1;0). Mặt phẳng (P):ax+by+cz-20 chứa đường thẳng AB và cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính giá trị của biểu thức M2a+b-c. A. M2. B. M3. C. M1. D. M4.
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): (x-1)²+ (y-2)²+ (z-3)²=25 và hai điểm A (3;-2;6), B (0;1;0). Mặt phẳng (P):ax+by+cz-2=0 chứa đường thẳng AB và cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính giá trị của biểu thức M=2a+b-c.
A. M=2.
B. M=3.
C. M=1.
D. M=4.
Trong không gian Oxyz cho mặt cầu (S): (x-3)²+ (y-1)²+z² 4 và đường thẳng
d
:
x
1
+
2
t
y
-
1
+
t
,...
Đọc tiếp
Trong không gian Oxyz cho mặt cầu (S): (x-3)²+ (y-1)²+z² = 4 và đường thẳng d : x = 1 + 2 t y = - 1 + t , t ∈ ℝ z = - t . Mặt phẳng chứa d và cắt (S) theo một đường tròn có bán kính nhỏ nhất có phương trình là:
A. 3x-2y-4z-8=0
B. y+z+1=0
C. x-2y-3=0
D. x+3y+5z+2=0
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;-2;3) và đường thẳng d có phương trình
x
+
1
2
y
-
2
1
z
+
3
-
1
Tính bán kính của mặt cầu (S) có tâm A và tiếp xúc với đường thẳng d
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;-2;3) và đường thẳng d có phương trình x + 1 2 = y - 2 1 = z + 3 - 1 Tính bán kính của mặt cầu (S) có tâm A và tiếp xúc với đường thẳng d
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho điểm
A
(
0
;
1
;
2
)
, mặt phẳng
α
:
x
-
y
+
z
-
4
0
và mặt cầu
S
:
(
x
-
3...
Đọc tiếp
Trong không gian Oxyz, cho điểm A ( 0 ; 1 ; 2 ) , mặt phẳng α : x - y + z - 4 = 0 và mặt cầu S : ( x - 3 ) 2 + ( y - 1 ) 2 + ( z - 2 ) 2 = 16 . Gọi (P) là mặt phẳng đi qua A, vuông góc với α và đồng thời (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tọa độ giao điểm M của (P) và trục x'Ox là:
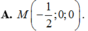
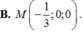
![]()
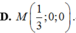
Trong không gian Oxyz, cho biết có hai mặt cầu có tâm nằm trên đường thẳng d:
x
2
y
-
1
1
z
+
2
-
1
, tiếp xúc đồng thời với 2 mặt phẳng:
(
α
)
: x+2...
Đọc tiếp
Trong không gian Oxyz, cho biết có hai mặt cầu có tâm nằm trên đường thẳng d: x 2 = y - 1 1 = z + 2 - 1 , tiếp xúc đồng thời với 2 mặt phẳng: ( α ) : x+2y-2z+1=0 và ( β ) : 2x-3y-6z-2=0. Gọi R 1 , R 2 ( R 1 > R 2 ) là bán kính 2 mặt cầu đó. Tỉ số R 1 R 2 bằng
A. 2
B. 3
C. 2
D. 4
Trong không gian với hệ tọa độ Oxyz, cho điểm A(0;1;2), mặt phẳng (α): x-y+z-40 và mặt cầu (S): (x-3)²+ (y-1)²+ (z-2)²16. Gọi (P) là mặt phẳng đi qua A, vuông góc với (α) và đồng thời (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tọa độ giao điểm M của (P) và trục xOx là:
A
.
M
-
1
2
;
0
;...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A(0;1;2), mặt phẳng (α): x-y+z-4=0 và mặt cầu (S): (x-3)²+ (y-1)²+ (z-2)²=16. Gọi (P) là mặt phẳng đi qua A, vuông góc với (α) và đồng thời (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tọa độ giao điểm M của (P) và trục x'Ox là:
A . M - 1 2 ; 0 ; 0
B . M - 1 3 ; 0 ; 0
C . M 1 ; 0 ; 0
D . M 1 3 ; 0 ; 0