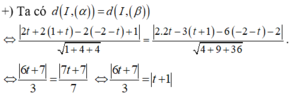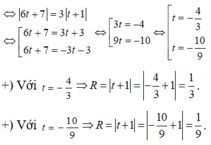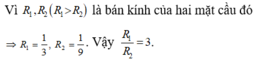Các câu hỏi tương tự
Trong không gian Oxyz, cho biết có hai mặt cầu có tâm cùng nằm trên đường thẳng
d
:
x
2
y
-
1
1
z
+
2
-
1
và tiếp xúc với mặt phẳng
(
α
)
:
x
+...
Đọc tiếp
Trong không gian Oxyz, cho biết có hai mặt cầu có tâm cùng nằm trên đường thẳng d : x 2 = y - 1 1 = z + 2 - 1 và tiếp xúc với mặt phẳng ( α ) : x + 2 y - 2 z + 1 = 0 ; ( β ) : 2 x - 3 y - 6 z - 2 = 0 có bán kính lần lượt bằng R 1 , R 2 ( R 1 > R 2 ) Tỉ số R 1 R 2 bằng
![]()
B. 3
C. 2
![]()
Trong không gian Oxyz cho các mặt phẳng (P): x - y + 2z + 1 0, (Q): 2x + y + z - 1 0. Gọi (S) là mặt cầu có tâm thuộc trục hoành, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và (S) cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính bằng r. Xác định r sao cho chỉ có đúng một mặt cầu (S) thỏa yêu cầu. A.
r
3
B.
r
3...
Đọc tiếp
Trong không gian Oxyz cho các mặt phẳng (P): x - y + 2z + 1= 0, (Q): 2x + y + z - 1 = 0. Gọi (S) là mặt cầu có tâm thuộc trục hoành, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và (S) cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính bằng r. Xác định r sao cho chỉ có đúng một mặt cầu (S) thỏa yêu cầu.
A. r = 3
B. r = 3 2
C. r = 2
D. r = 3 2 2
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng
(
P
)
:
x
−
y
+
2
z
+
1
0
và
(
Q
)
:
2
x
+
y
+
z
−
z
0.
Gọi (S) là mặt cầu có tâm thuộc Ox, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và cắt mặt phẳng (Q)...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng ( P ) : x − y + 2 z + 1 = 0 và ( Q ) : 2 x + y + z − z = 0. Gọi (S) là mặt cầu có tâm thuộc Ox, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính r. Xác định r sao cho chỉ có duy nhất một mặt cầu (S) thỏa mãn điều kiện bài toán
A. r = 3 2 2 .
B. r = 10 2 .
C. r = 3 .
D. r = 14 2 .
Trong không gian tọa độ Oxyz, cho mặt cầu (S):
(
x
-
2
)
2
+
y
2
+
(
z
+
1
)
2
9
và mặt phẳng (P): 2x-y-2z-30. Biết rằng mặt cầu (S) cắt (P) theo giao tuyến là đường tròn...
Đọc tiếp
Trong không gian tọa độ Oxyz, cho mặt cầu (S): ( x - 2 ) 2 + y 2 + ( z + 1 ) 2 = 9 và mặt phẳng (P): 2x-y-2z-3=0. Biết rằng mặt cầu (S) cắt (P) theo giao tuyến là đường tròn (C). Tính bán kính R của (C)
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng (P): 2x-y-2z-20 và mặt phẳng (Q): 2x-y-2z+100 song song với nhau. Biết A(1;2;1) là điểm nằm giữa hai mặt phẳng (P) và (Q). Gọi (S) là mặt cầu qua A và tiếp xúc với cả hai mặt phẳng (P) và (Q). Biết rằng khi (S) thay đổi thì tâm của nó luôn nằm trên một đường tròn. Tính bán kính r của đường tròn đó A.
r
4
2...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng (P): 2x-y-2z-2=0 và mặt phẳng (Q): 2x-y-2z+10=0 song song với nhau. Biết A(1;2;1) là điểm nằm giữa hai mặt phẳng (P) và (Q). Gọi (S) là mặt cầu qua A và tiếp xúc với cả hai mặt phẳng (P) và (Q). Biết rằng khi (S) thay đổi thì tâm của nó luôn nằm trên một đường tròn. Tính bán kính r của đường tròn đó
A. r = 4 2 3
B. r = 2 2 3
C. r = 5 3
D. r = 2 5 3
Trong không gian với hệ tọa độ Oxyz, cho các mặt phẳng
P
:
2
x
−
y
−
z
−
2
0
;
Q
:
x
−
2
y
+
z
+
2
0
;
R
:
x
+
y
−
2
z
+
2
0
,...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho các mặt phẳng P : 2 x − y − z − 2 = 0 ; Q : x − 2 y + z + 2 = 0 ; R : x + y − 2 z + 2 = 0 , T : x + y + z = 0 . Hỏi có bao nhiêu mặt cầu có tâm thuộc (T) và tiếp xúc với P , Q , R ?
A. 1
B. 2
C. 3
D. 4
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
d
:
x
-
1
1
y
+
2
1
z
1
và mặt phẳng (P): 2x+y-2z+20. Gọi (S) là mặt cầu có tâm nằm trên d, tiếp xúc với mặt phẳng (P) và đi qua điểm A(2;-1;0). Biết tâm của mặt cầu có cao độ không nhỏ hơn 1,...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x - 1 1 = y + 2 1 = z 1 và mặt phẳng (P): 2x+y-2z+2=0. Gọi (S) là mặt cầu có tâm nằm trên d, tiếp xúc với mặt phẳng (P) và đi qua điểm A(2;-1;0). Biết tâm của mặt cầu có cao độ không nhỏ hơn 1, phương trình mặt cầu (S) là:
![]()
![]()
![]()
![]()
Trong không gian Oxyz, xét số thực
m
∈
(
0
;
1
)
và hai mặt phẳng (
α
): 2x-y+2z+100 và (
β
):
x
m
+
y
1
-
m
+
z
1
1
Biết rằng, khi m thay đổi có hai mặt cầu cố định tiếp xúc đồng thời với cả hai mặt phẳng...
Đọc tiếp
Trong không gian Oxyz, xét số thực m ∈ ( 0 ; 1 ) và hai mặt phẳng ( α ): 2x-y+2z+10=0 và ( β ): x m + y 1 - m + z 1 = 1 Biết rằng, khi m thay đổi có hai mặt cầu cố định tiếp xúc đồng thời với cả hai mặt phẳng ( α ),( β ). Tổng bán kính của hai mặt cầu đó bằng
A. 6
B. 3
C. 9
D. 12
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (0; 2; 2), B (2; -2; 0). Gọi I1 (1; 1; -1) và I2 (3; 1; 1) là tâm của hai đường tròn nằm trên hai mặt phẳng khác nhau và có chung một dây cung AB. Biết rằng luôn có một mặt cầu (S) đi qua cả hai đường tròn ấy. Tính bán kính R của (S).
A
.
R
219
3
B. R 2
2
C
.
R...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (0; 2; 2), B (2; -2; 0). Gọi I1 (1; 1; -1) và I2 (3; 1; 1) là tâm của hai đường tròn nằm trên hai mặt phẳng khác nhau và có chung một dây cung AB. Biết rằng luôn có một mặt cầu (S) đi qua cả hai đường tròn ấy. Tính bán kính R của (S).
A . R = 219 3
B. R = 2 2
C . R = 129 3
D. R = 2 6