Có ![]()
![]() và tứ diện O.ABC vuông tại O nên:
và tứ diện O.ABC vuông tại O nên:
![]()

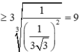
![]()
Chọn đáp án B. Mẹo TN: Vì tính đối xứng cho

![]()
Chọn đáp án B.
Có ![]()
![]() và tứ diện O.ABC vuông tại O nên:
và tứ diện O.ABC vuông tại O nên:
![]()

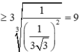
![]()
Chọn đáp án B. Mẹo TN: Vì tính đối xứng cho

![]()
Chọn đáp án B.
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A a ; 0 ; 0 , B 0 ; b ; 0 , C 0 ; 0 ; c với a, b, c là những số dương thay đổi sao cho a 2 + b 2 + c 2 = 3 . Khi khoảng cách từ O đến mặt phẳng (ABC) là lớn nhất, tổng a + b + c là
A. 1
B. 3
C. 2
D. 3 2
Trong không gian với hệ toạ độ Oxyz, xét ba điểm A(a;0;0),B(0;b;0),C(0;0;c) với a,b,c là các số thực thay đổi thoả mãn 1 a - 2 b + 2 c = 1 . Biết rằng mặt cầu (S): ( x - 2 ) 2 + y 2 + ( z - 4 ) 2 = 25 cắt mặt phẳng (ABC) theo giao tuyến là một đường tròn có bán kính bằng 4. Giá trị của biểu thức a+b+c bằng
A. 5.
B. 1.
C. 2.
D. 4.
Trong không gian Oxyz, cho ba điểm A(a;0;0), B(0;b;0), C(0;0;c) với a, b, c là những số thực dương thay đổi sao cho a2 + 4b2 + 16c2 = 49. Tính tổng F = a2 + b2 +c2 sao cho khoảng cách từ O đến (ABC) là lớn nhất.
A. F = 51 5
B. F = 51 4
C. F = 49 5
D. F = 49 4
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) cắt ba trục tọa độ lần lượt là A(a;0;0), B(0;b;0), C(0;0;c) với a b c ≠ 0 thỏa mãn 2 a + b = a b 2 c + 1 - 1 b . Khoảng cách lớn nhất từ O đến mặt phẳng (P) là:
A. 7
B. 17
C. 3
D. 1 17
Trong không gian với hệ toạ độ Oxyz, xét ba điểm A a ; 0 ; 0 , B 0 ; b ; 0 , C 0 ; 0 ; c với a,b,c là các số thực thay đổi thoả mãn 1 a - 2 b + 2 c = 1 Biết rằng mặt cầu S : x - 2 2 + y 2 + z - 4 2 = 25 cắt mặt phẳng (ABC) theo giao tuyến là một đường tròn có bán kính bằng 4. Giá trị của biểu thức a + b + c bằng
A. 5.
B. 1.
C. 2.
D. 4.
Trong không gian với hệ toạ độ Oxyz, xét các điểm A a ; 0 ; 0 , B 0 ; b ; 0 , C 0 ; 0 ; c , với abc > 0 và a + 2 b + 2 c = 6 . Biết rằng khi a, b, c thay đổi thì quỹ tích tâm mặt cầu ngoại tiếp tứ diện OABC thuộc mặt phẳng (P) cố định. Tính khoảng cách từ điểm O tới mặt phẳng (P)
A. 1
B. 3
C. 2
D. 3
Trong hệ tục toạ độ không gian Oxyz, cho A(1;0;0), B(0;b;0), C(0;0;c), biết b,c>0, phương trình mặt phẳng (P): y-z+1= 0. Tính M=b+c biết (ABC) ⊥ (P),d(O;(ABC))=1/3
A. 2
B. 1/2
C. 5/2
D. 1
Trong không gian với hệ tọa độ Oxyz, cho 3 điểm A(a;0;0), B(1;b;0), C(1;0;c), với a,b,c là các số thực thay đổi sao cho H(3;2;1) là trực tâm của tam giác ABC. Tính S=a+b+c.
A. S = 2
B. S = 19
C. S = 11
D. S = 9
Trong không gian với hệ tọa độ Oxyz, cho các điểm A(–1; –2;0), B(0; –4;0), C(0;0; –3). Phương trình mặt phẳng (P) nào dưới đây đi qua A, gốc tọa độ O và cách đều hai điểm B và C?
A. (P): 6x – 3y + 5z = 0
B. (P): 6x – 3y + 4z = 0
C. (P): 2x – y – 3z = 0
D. (P): 2x – y + 3z = 0