Đáp án C
Mặt cầu (S) chính là mặt cầu nội tiếp hình lập phương cạnh a ⇒ R = a 2 .
Vậy thể tích khối cầu (S) là V = 4 3 π R 3 = 4 3 π . a 2 3 = π a 3 6 .
Đáp án C
Mặt cầu (S) chính là mặt cầu nội tiếp hình lập phương cạnh a ⇒ R = a 2 .
Vậy thể tích khối cầu (S) là V = 4 3 π R 3 = 4 3 π . a 2 3 = π a 3 6 .
Cho mặt cầu (S) có bán kính bằng 3 (m), đường kính AB. Qua A và B dựng các tia A t 1 , B t 2 tiếp xúc với mặt cầu và vuông góc với nhau. M và N là hai điểm lần lượt di chuyển trên A t 1 , B t 2 sao cho MN cũng tiếp xúc với (S). Biết rằng khối tứ diện ABMN có thể tích V m 3 không đổi. V thuộc khoảng nào sau đây?
A. (17;21)
B. (15;17)
C. (25;28)
D. (23;25)
Một khối đa diện (H) được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ. Gọi (S) là khối cầu có thể tích lớn nhất chứa trong (H) và tiếp xúc với các mặt (A'B'C'D'),(BCC'B'),(DCC'D'). Tính bán kính của (S).
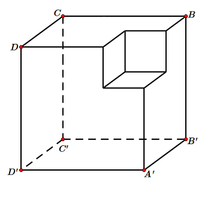
A. 2 + 3 3
B. 3 - 3
C. 2 3 3
D. 2
Trong không gian với hệ tọa độ Oxyz cho 4 điểm A(3;-2;-2), B93;2;0), C(0;2;1), D(-1;1;2). Phương trình mặt cầu (S) tâm A và tiếp xúc với mặt phẳng (BCD) là
A. x - 3 2 + y + 2 2 + z + 2 2 = 14
B. x + 3 2 + y + 2 2 + z + 2 2 = 14
C. x - 3 2 + y - 2 2 + z + 2 2 = 14
D. x - 3 2 + y + 2 2 + z - 2 2 = 14
Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A ( a ; 0 ; 0 ) , B ( 0 ; b ; 0 ) , C ( 0 ; 0 ; c ) , trong đó a > 0 , b > 0 , c > 0 và 3 a + 1 b + 3 c = 5 . Biết mặt phẳng (ABC) tiếp xúc với mặt cầu (S) có phương trình là ( x - 3 ) 2 + ( y - 1 ) 2 + ( z - 3 ) 2 = 304 25 , khi đó thể tích của khối tứ diện OABC nằm trong khoảng nào?
A . ( 0 ; 1 2 ) .
B. (0;1).
C. (1;3).
D. (4;5).
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 = 3. Một mặt phẳng α tiếp xúc với mặt cầu (S) và cắt các tia Ox, Oy, Oz lần lượt tại A, B, C và thỏa mãn O A 2 + O B 2 + O C 2 = 27. Diện tích của tam giác ABC bằng
A. 3 3 2
B. 9 3 2
C. 3 3
D. 9 3
Tính thể tích khối cầu nội tiếp hình lập phương cạnh a (khối cầu tiếp xúc với tất cả các mặt của hình lập phương).
A. π a 3 2 6
B. π a 3 6
C. π a 3 8
D. π a 3 6
Trong không gian cho ABCD là hình chữ nhật, AB=2, AD=1. Đường thẳng d nằm trong mặt phẳng (ABCD) không có điểm chung với hình chữ nhật ABCD, song song với cạnh AB và cách AB một khoảng bằng a. Gọi V là thể tích của khối tròn xoay T, nhận được khi quay hình chữ nhật ABCD xung quanh trục d. Cho biết d ( A B , d ) < d ( C D , d ) . Tính a biết rằng thể tích khối T gấp 3 lần thể tích của khối cầu có đường kính AB.
A. a = 3
B. a = - 1 + 2
C. a = 1 2
D. a = 15 2
Một hình lập phương có diện tích mặt chéo bằng a 2 2 . Gọi V là thể tích khối cầu và S là diện tích mặt cầu ngoại tiếp hình lập phương nói trên. Khi đó tích S.V bằng
A. S V = 3 π 2 a 5 2
B. S V = 3 3 π 2 a 5 2
C. S V = 3 6 π 2 a 5 2
D. S V = 3 π 2 a 5 2
Trong không gian với hệ tọa độ Oxyz cho mặt cầu S : x 2 + y 2 + z 2 = 3 . Một mặt phẳng α tiếp xúc với mặt cầu (S) và cắt các tia Ox, Oy, Oz tương ứng tại A, B, C. Tính giá trị của biểu thức T = 1 O A 2 + 1 O B 2 + 1 O C 2
A. T = 1 3
B. T = 1 3
C. T = 1 9
D. T = 3