Các câu hỏi tương tự
Trong không gian mặt cầu (S) tiếp xúc với 6 mặt của một hình lập phương cạnh a, thể tích khối cầu (S) bằng A.
V
π
a
3
24
B.
V
π
a
3
3
C.
V
π
a...
Đọc tiếp
Trong không gian mặt cầu (S) tiếp xúc với 6 mặt của một hình lập phương cạnh a, thể tích khối cầu (S) bằng
A. V = π a 3 24
B. V = π a 3 3
C. V = π a 3 6
D. V = 4 3 π a 3
Cho hình lập phương có cạnh bằng a. Tính theo a thể tích của khối cầu tiếp xúc với 12 cạnh của hình lập phương đó. A.
π
a
3
6
B.
4
π
a
3
3
C.
π
2
a
3...
Đọc tiếp
Cho hình lập phương có cạnh bằng a. Tính theo a thể tích của khối cầu tiếp xúc với 12 cạnh của hình lập phương đó.
A. π a 3 6
B. 4 π a 3 3
C. π 2 a 3 3
D. π 3 a 3 2
Tính thể tích V của khối cầu tiếp xúc với tất cả các cạnh của hình lập phương cạnh
2
2
A.
V
32
π
3
B.
V
32
π
6
C.
V
256
π
6
D.
V...
Đọc tiếp
Tính thể tích V của khối cầu tiếp xúc với tất cả các cạnh của hình lập phương cạnh 2 2
A. V = 32 π 3
B. V = 32 π 6
C. V = 256 π 6
D. V = 64 π 2 3
Cho hình lập phương cạnh 4cm. Trong khối lập phương là khối cầu tiếp xúc với các mặt của hình lập phương. Tính thể tích phần còn lại của khối lập phương. A.
64
-
64
2
3
π
cm
3
B.
64
-
32
3
π
cm
3
C.
64
-...
Đọc tiếp
Cho hình lập phương cạnh 4cm. Trong khối lập phương là khối cầu tiếp xúc với các mặt của hình lập phương. Tính thể tích phần còn lại của khối lập phương.
A. 64 - 64 2 3 π cm 3
B. 64 - 32 3 π cm 3
C. 64 - 32 3 π cm 3
D. 64 - 256 81 π cm 3
Cho một hình lập phương có bán kính mặt cầu ngoại tiếp, mặt cầu nội tiếp và mặt cầu tiếp xúc với tất cả các cạnh của hình lập phương lần lượt là
R
1
,
R
2
,
R
3
. Mệnh đề nào sau đây đúng? A.
R
1
R
3
R
2
B. ...
Đọc tiếp
Cho một hình lập phương có bán kính mặt cầu ngoại tiếp, mặt cầu nội tiếp và mặt cầu tiếp xúc với tất cả các cạnh của hình lập phương lần lượt là R 1 , R 2 , R 3 . Mệnh đề nào sau đây đúng?
A. R 1 > R 3 > R 2
B. R 1 > R 2 > R 3
C. R 3 > R 1 > R 2
D. R 2 > R 1 > R 3
Một hình lập phương cạnh bằng a nội tiếp khối cầu
S
1
và ngoại tiếp khối cầu
S
2
, gọi
V
1
và
V
2
lần lượt là thể tích của các khối
S
1
và
S
2
. Tính tỉ số
k...
Đọc tiếp
Một hình lập phương cạnh bằng a nội tiếp khối cầu S 1 và ngoại tiếp khối cầu S 2 , gọi V 1 và V 2 lần lượt là thể tích của các khối S 1 và S 2 . Tính tỉ số k = V 1 V 2 .
A. k = 1 2 2
B. k = 1 3 3
C. k = 2 2
D. 3 3
Một hình lập phương có cạnh bằng 2a vừa nội tiếp hình trụ (T) vừa nội tiếp mặt cầu (C) và hai đáy của hình lập phương nằm trên 2 đáy của hình trụ. Tính tỉ số thể tích
V
C
V
T
giữa khối cầu và khối trụ giới hạn bởi (C) và (T) ? A.
V
C
V...
Đọc tiếp
Một hình lập phương có cạnh bằng 2a vừa nội tiếp hình trụ (T) vừa nội tiếp mặt cầu (C) và hai đáy của hình lập phương nằm trên 2 đáy của hình trụ. Tính tỉ số thể tích V C V T giữa khối cầu và khối trụ giới hạn bởi (C) và (T) ?
A. V C V T = 2 2
B. V C V T = 3
C. V C V T = 2
D. V C V T = 3 2
Cho hình lập phương cạnh a. Gọi V1, V2 lần lượt là thể tích của mặt cầu ngoại tiếp, nội tiếp của hình lập phương. Tính tỷ số
V
1
V
2
A.
3
B. 2
3
C. 2 D. 3
3
Đọc tiếp
Cho hình lập phương cạnh a. Gọi V1, V2 lần lượt là thể tích của mặt cầu ngoại tiếp, nội tiếp của hình lập phương. Tính tỷ số V 1 V 2
A. 3
B. 2 3
C. 2
D. 3 3
Một khối đa diện (H) được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ. Gọi (S) là khối cầu có thể tích lớn nhất chứa trong (H) và tiếp xúc với các mặt (ABCD),(BCCB),(DCCD). Tính bán kính của (S). A.
2
+
3
3
B.
3
-
3
C.
2...
Đọc tiếp
Một khối đa diện (H) được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ. Gọi (S) là khối cầu có thể tích lớn nhất chứa trong (H) và tiếp xúc với các mặt (A'B'C'D'),(BCC'B'),(DCC'D'). Tính bán kính của (S).
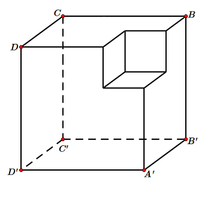
A. 2 + 3 3
B. 3 - 3
C. 2 3 3
D. 2




