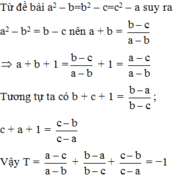Các câu hỏi tương tự
Cho a,b,c đôi một khác nhau thỏa mãn: \(a^2+b=b^2+c=c^2+a\). Tính \(T=\left(a+b-1\right)\left(b+c-1\right)\left(c+a-1\right)\)
cho ba số thực phân biệt a,b,c thỏa mãn `a^2 -ab=b^2 -bc=c^2 -ca`. Tính \(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\)
Không cần giải hết ạ T^T Giải đc 1 bài là em cảm kích lắm rùiBài 1: Cho a,b,c là 3 số dương. Chứng minh rằng:frac{a^2}{b+c}+frac{b^2}{c+a}+frac{c^2}{a+b}geqfrac{a+b+c}{2}Bài 2:a) Cho x0, y0 thỏa mãn x^2+y^24. Tìm giá trị lớn nhất của biểu thức:Pfrac{xy}{x+y+2}b) Cho p là số nguyên tố (p2). Chứng minh rằng số 2/p chỉ có thể biểu diễn dưới dạng duy nhất frac{2}{p}frac{1}{x}+frac{1}{y}(Trong đó x, y là các số nguyên dương phân biệt)
Đọc tiếp
Không cần giải hết ạ T^T Giải đc 1 bài là em cảm kích lắm rùi
Bài 1: Cho a,b,c là 3 số dương. Chứng minh rằng:
\(\frac{a^2}{b+c}+\frac{b^2}{c+a}+\frac{c^2}{a+b}\geq\frac{a+b+c}{2}\)
Bài 2:
a) Cho x>0, y>0 thỏa mãn \(x^2+y^2=4\). Tìm giá trị lớn nhất của biểu thức:
\(P=\frac{xy}{x+y+2}\)
b) Cho p là số nguyên tố (p>2). Chứng minh rằng số 2/p chỉ có thể biểu diễn dưới dạng duy nhất \(\frac{2}{p}=\frac{1}{x}+\frac{1}{y}\)
(Trong đó x, y là các số nguyên dương phân biệt)
Cho 3 số đôi một khác nhau thỏa mãn: \(a^2+b=b^2+c=c^2+a.\)
Tính \(T=\left(a+b-1\right)\left(b+c-1\right)\left(c+a-1\right).\)
Cho 3 số thực không âm a,b,c thỏa mãn \(a^2+b^2+c^2=2\left(a+b++c\right)\)
Tìm max T = \(\frac{a}{a+1}+\frac{b}{b+1}+\frac{c}{c+1}\)
1. Phân tích đa thức thành nhân tử:x^5-x^4+left(y+2right)x^3+left(y-2right)x^2+yx+y^22. Cho các số dương thỏa mãn:dfrac{b+c}{a^2}+dfrac{c+a}{b^2}+dfrac{a+b}{c^2}2left(dfrac{1}{a}+dfrac{1}{b}+dfrac{1}{c}right)Tính giá trị biểu thức sau: Pleft(a-bright)^{2009}+left(b-cright)^{2009}+left(c-aright)^{2009}3. Cho x,y,x đôi một khác nhau và khác 0. Chứng minh rằng nếu:dfrac{x^2-yz}{a}dfrac{y^2-xz}{b}dfrac{z^2-xy}{c} thì ta có:dfrac{a^2-bc}{x}dfrac{b^2-ca}{y}dfrac{c^2-ab}{z}
Đọc tiếp
1. Phân tích đa thức thành nhân tử:
\(x^5-x^4+\left(y+2\right)x^3+\left(y-2\right)x^2+yx+y^2\)
2. Cho các số dương thỏa mãn:
\(\dfrac{b+c}{a^2}+\dfrac{c+a}{b^2}+\dfrac{a+b}{c^2}=2\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\)
Tính giá trị biểu thức sau: \(P=\left(a-b\right)^{2009}+\left(b-c\right)^{2009}+\left(c-a\right)^{2009}\)
3. Cho x,y,x đôi một khác nhau và khác 0. Chứng minh rằng nếu:
\(\dfrac{x^2-yz}{a}=\dfrac{y^2-xz}{b}=\dfrac{z^2-xy}{c}\) thì ta có:
\(\dfrac{a^2-bc}{x}=\dfrac{b^2-ca}{y}=\dfrac{c^2-ab}{z}\)
Cho 3 số thực không âm a,b,c thỏa mãn \(a^2+b^2+c^2=2\left(a+b+c\right)\)
Tìm min của \(T=\frac{a}{a+1}+\frac{b}{b+1}+\frac{c}{c+1}\)
1/tìm các cặp nguyên dương ( x;y) thỏa PT
X^2 + X + 13 = Y^2
2/ tiện giúp lun T^T
a,b,c > 0 thỏa 1/(1+a) + 1/(1+b) + 1/(1+c) >hoặc = 2
CMR: abc < hoặc = 1/2
Cho 3 số thực không âm a,b,c thỏa mãn a2+b2+c2=2(a+b+c) . Tìm giá trị lớn nhất của biểu thức \(T=\frac{a}{a+1}+\frac{b}{b+1}+\frac{c}{c+1}\)