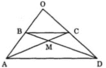
Kẻ AH⊥DC tại H, BK⊥DC tại K, DN⊥AB tại N; CM⊥AB tại M
=>AH,BK,DN,CM là các đường cao của hình thang ABCD
Xét hình thang ABCD có AH là đường cao
nên \(S_{ABCD}=\frac12\times AH\times\left(AB+CD\right)\left(1\right)\)
Xét hình thang ABCD có BK là đường cao
nên \(S_{ABCD}=\frac12\times BK\times\left(BA+CD\right)\left(2\right)\)
Xét hình thang ABCD có CM là đường cao
nên \(S_{ABCD}=\frac12\times CM\times\left(AB+CD\right)\left(3\right)\)
Xét hình thang ABCD có DN là đường cao
nên \(S_{ABCD}=\frac12\times DN\times\left(AB+CD\right)\) (4)
Từ (1),(2),(3),(4) suy ra AH=BK=CM=DN
Xét ΔADC có AH là đường cao
nên \(S_{ADC}=\frac12\times AH\times DC\) (5)
Xét ΔBDC có BK là đường cao
nên \(S_{BDC}=\frac12\times BK\times DC=\frac12\times AH\times DC\) (6)
Từ (5),(6) suy ra \(S_{ADC}=S_{BDC}\)
Xét ΔDAB có DN là đường cao
nên \(S_{DAB}=\frac12\times DN\times AB\) (7)
Xét ΔCAB có CM là đường cao
nên \(S_{CAB}=\frac12\times CM\times AB\) (8)
Từ (7),(8) suy ra \(\frac{S_{DAB}}{S_{CAB}}=\frac{\frac12\cdot DN\cdot AB}{\frac12\cdot CM\cdot AB}=\frac{DN}{CM}=1\)
=>\(S_{DAB}=S_{CAB}\)