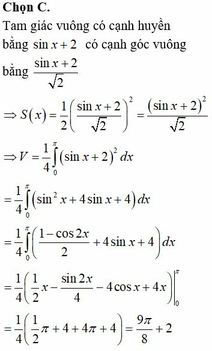Các câu hỏi tương tự
Thể tích V của vật thể nằm giữa hai mặt phẳng x 0 và
x
π
, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x
(
0
≤
x
≤
π
)
là một tam giác đều cạnh A. V 3 B. V 3
π
C.
2
3
D.
2
π
3
Đọc tiếp
Thể tích V của vật thể nằm giữa hai mặt phẳng x = 0 và x = π , biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x ( 0 ≤ x ≤ π ) là một tam giác đều cạnh
A. V = 3
B. V = 3 π
C. 2 3
D. 2 π 3
Tính thể tích V của vật thể nằm giữa hai mặt phẳng x 0 và x
π
, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ
x
0
≤
x
≤
π
là một tam giác đều cạnh là
2
sin
x
A.
V
3
B.
V
3
π...
Đọc tiếp
Tính thể tích V của vật thể nằm giữa hai mặt phẳng x = 0 và x = π , biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x 0 ≤ x ≤ π là một tam giác đều cạnh là 2 sin x
A. V = 3
B. V = 3 π
C. V = - 2 π 3
D. V = 2 3
Tính thể tích V của vật thể nằm giữa hai mặt phẳng x 0 và
x
π
,
biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ
x
0
≤
x
≤
π
là một tam giác đều cạnh là
2
s
i
n
x
A.
V
...
Đọc tiếp
Tính thể tích V của vật thể nằm giữa hai mặt phẳng x = 0 và x = π , biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x 0 ≤ x ≤ π là một tam giác đều cạnh là 2 s i n x
A. V = 3
B. V = 3 π
C. V = 2 π 3
D. V = 2 3
Tính thể tích của vật thể nằm giữa hai mặt phẳng
x
0
;
x
π
, biết rằng thiết diện của vật thể với mặt phẳng vuông góc với trục Ox tại điểm có hoành độ
x
∈
0
;
π
là một tam giác đều có cạnh là
2
sin
x
A.
3
B.
π...
Đọc tiếp
Tính thể tích của vật thể nằm giữa hai mặt phẳng x = 0 ; x = π , biết rằng thiết diện của vật thể với mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x ∈ 0 ; π là một tam giác đều có cạnh là 2 sin x
A. 3
B. π 3
C. 2 3
D. 2 π
Cho một vật thể nằm giữa hai mặt phẳng x0,
x
π
biết rằng mặt phẳng vuông góc với trục Ox tại điểm có hoành độ
x
0
≤
x
≤
π
cắt vật thể theo thiết diện là một tam giác đều cạnh
2
sin
x
Thể tích của vật thể đó là A.
3
π
2
B.
2...
Đọc tiếp
Cho một vật thể nằm giữa hai mặt phẳng x=0, x = π biết rằng mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x 0 ≤ x ≤ π cắt vật thể theo thiết diện là một tam giác đều cạnh 2 sin x Thể tích của vật thể đó là
A. 3 π 2
B. 2 3
C. 3 2
D. 2 π 3
Cho phần vật thể (T) giới hạn bởi hai mặt phẳng có phương trình x 0 và x 2 Cắt phần vật thể (T) bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ
0
≤
x
≤
2
,
ta được thiết diện là một tam giác đều có độ dài cạnh bằng
x
2
-
x
.
Tính thể tích V của phần vật thể (T). A.
V...
Đọc tiếp
Cho phần vật thể (T) giới hạn bởi hai mặt phẳng có phương trình x = 0 và x = 2 Cắt phần vật thể (T) bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ 0 ≤ x ≤ 2 , ta được thiết diện là một tam giác đều có độ dài cạnh bằng x 2 - x . Tính thể tích V của phần vật thể (T).
A. V = 4 3 .
B. V = 3 3 .
C. V = 4 3 .
D. V = 3 .
Cho phần vật thể (T) giới hạn bởi hai mặt phẳng có phương trình x 0 và x 2. Cắt phần vật thể (T) bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ
x
0
≤
x
≤
2
,
, ta được thiết diện là một tam giác đều có độ dài cạnh bằng
x
2
−
x...
Đọc tiếp
Cho phần vật thể (T) giới hạn bởi hai mặt phẳng có phương trình x = 0 và x = 2. Cắt phần vật thể (T) bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x 0 ≤ x ≤ 2 , , ta được thiết diện là một tam giác đều có độ dài cạnh bằng x 2 − x . Tính thể tích V của phần vật thể (T).
A. V = 4 3 .
B. V = 3 3 .
C. V = 4 3 .
D. V = 3 .
Cho phần vật thể A giới hạn bởi hai mặt phẳng
x
0
;
x
1
cắt phần vật thể B bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ
x
0
≤
x
≤
1
ta được thiết diện là một tam giác đều có độ dài canh bằng
x
1
−
x
.
Tính thể t...
Đọc tiếp
Cho phần vật thể A giới hạn bởi hai mặt phẳng x = 0 ; x = 1 cắt phần vật thể B bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x 0 ≤ x ≤ 1 ta được thiết diện là một tam giác đều có độ dài canh bằng x 1 − x . Tính thể tích phần vật thể B.
A. 3 4
B. 3 48
C. 3 6
D. 3 12
Tính thể tích vật thể bị giới hạn bởi các mặt phẳng x 0 và x 1, biết thiết diện của vật thể khi cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ
x
0
≤
x
≤
1
là một hình vuông có độ dài cạnh
x
e
x
-
1
. A....
Đọc tiếp
Tính thể tích vật thể bị giới hạn bởi các mặt phẳng x = 0 và x =1, biết thiết diện của vật thể khi cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x 0 ≤ x ≤ 1 là một hình vuông có độ dài cạnh x e x - 1 .
A. V = π 2
B. V = e - 1 2
C. V = 1 2
D. V = π e - 1 2