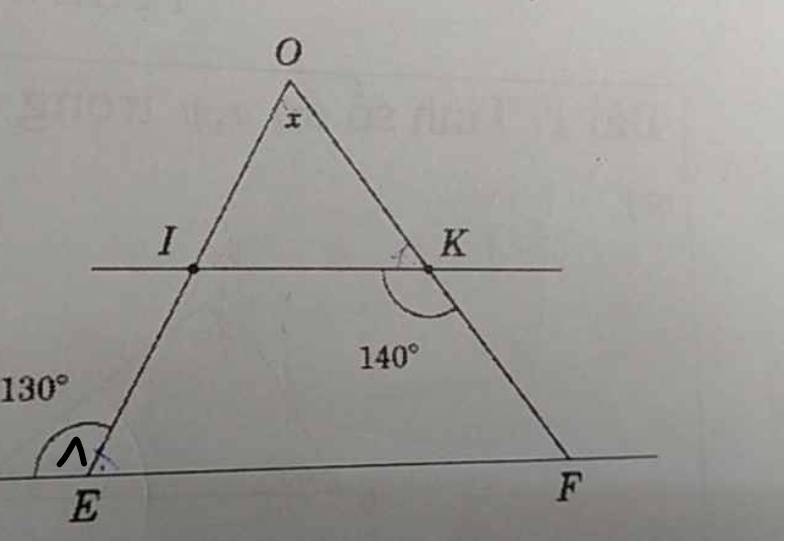
IK//EF
=>\(\widehat{IKF}+\widehat{OFE}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{OFE}+140^0=180^0\)
=>\(\widehat{OFE}=40^0\)
\(\widehat{IEF}+\widehat{E_1}=180^0\)(hai góc kề bù)
=>\(\widehat{IEF}+130^0=180^0\)
=>\(\widehat{IEF}=50^0\)
Xét ΔOEF có \(\widehat{EOF}+\widehat{FEO}+\widehat{EFO}=180^0\)
=>\(x+50^0+40^0=180^0\)
=>\(x=90^0\)
Lời giải:
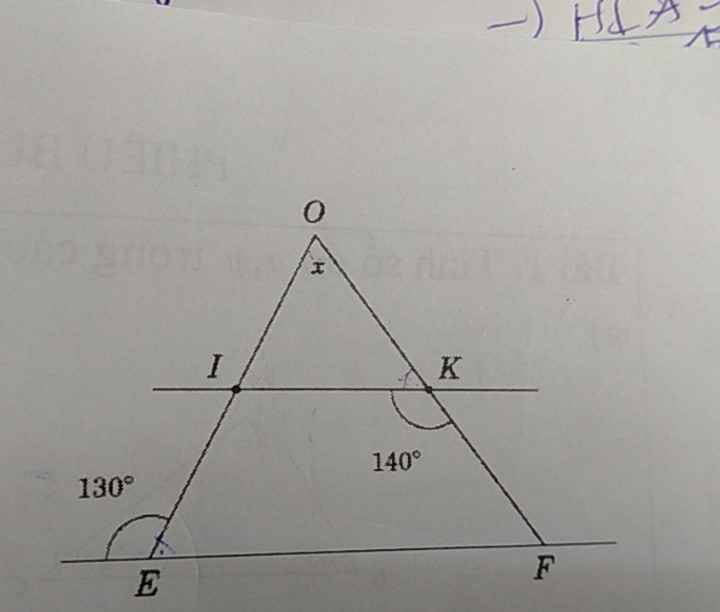
Bổ sung điều kiện: $IK\parallel EF$.
Vì $IK\parallel EF$ nên:
$\widehat{OIK}=\widehat{OEF}$ (2 góc đồng vị)
$=180^0-130^0=50^0$
$\widehat{OKI}=180^0-\widehat{IKF}=180^0-140^0=40^0$
Xét tam giác $OIK$ thì:
$x=180^0-(\widehat{OIK}+\widehat{OKI})=180^0-(50^0+40^0)=90^0$






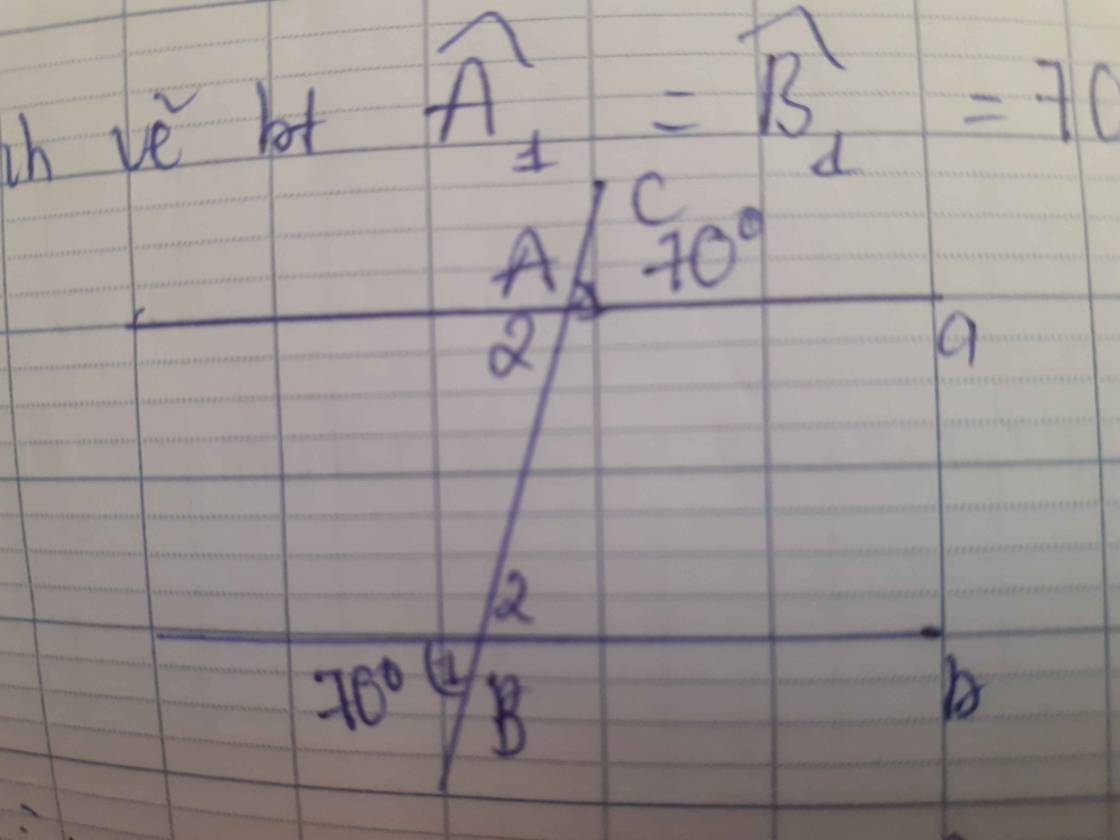


 bn nào làm hộ mình với mình đang cần gấp.
bn nào làm hộ mình với mình đang cần gấp.





