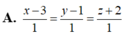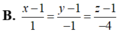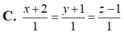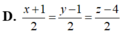(d): \(\left\{{}\begin{matrix}x=2-2t\\y=1-2t\\z=1+t\end{matrix}\right.\)
=>(d) có vecto chỉ phương là \(\overrightarrow{a}=\left(-2;-2;1\right)\)
(d'): Đặt \(\dfrac{x+2}{1}=\dfrac{y+4}{2}=\dfrac{z+1}{2}=k\)
=>\(\left\{{}\begin{matrix}x+2=k\\y+4=2k\\z+1=2k\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2+k\\y=-4+2k\\z=-1+2k\end{matrix}\right.\)
=>(d') có vecto chỉ phương là \(\overrightarrow{b}=\left(1;2;2\right)\)
Gọi góc giữa (d) và (d') là \(\alpha\)
\(cos\alpha=\dfrac{\left|-2\cdot1+\left(-2\right)\cdot2+1\cdot2\right|}{\sqrt{\left(-2\right)^2+\left(-2\right)^2+1^2}\cdot\sqrt{1^2+2^2+2^2}}=\dfrac{\left|-2-4+2\right|}{\sqrt{4+4+1}\cdot\sqrt{4+4+1}}=\dfrac{\left|-4\right|}{3\cdot3}=\dfrac{4}{9}\)
=>\(\alpha\simeq63^037'\)