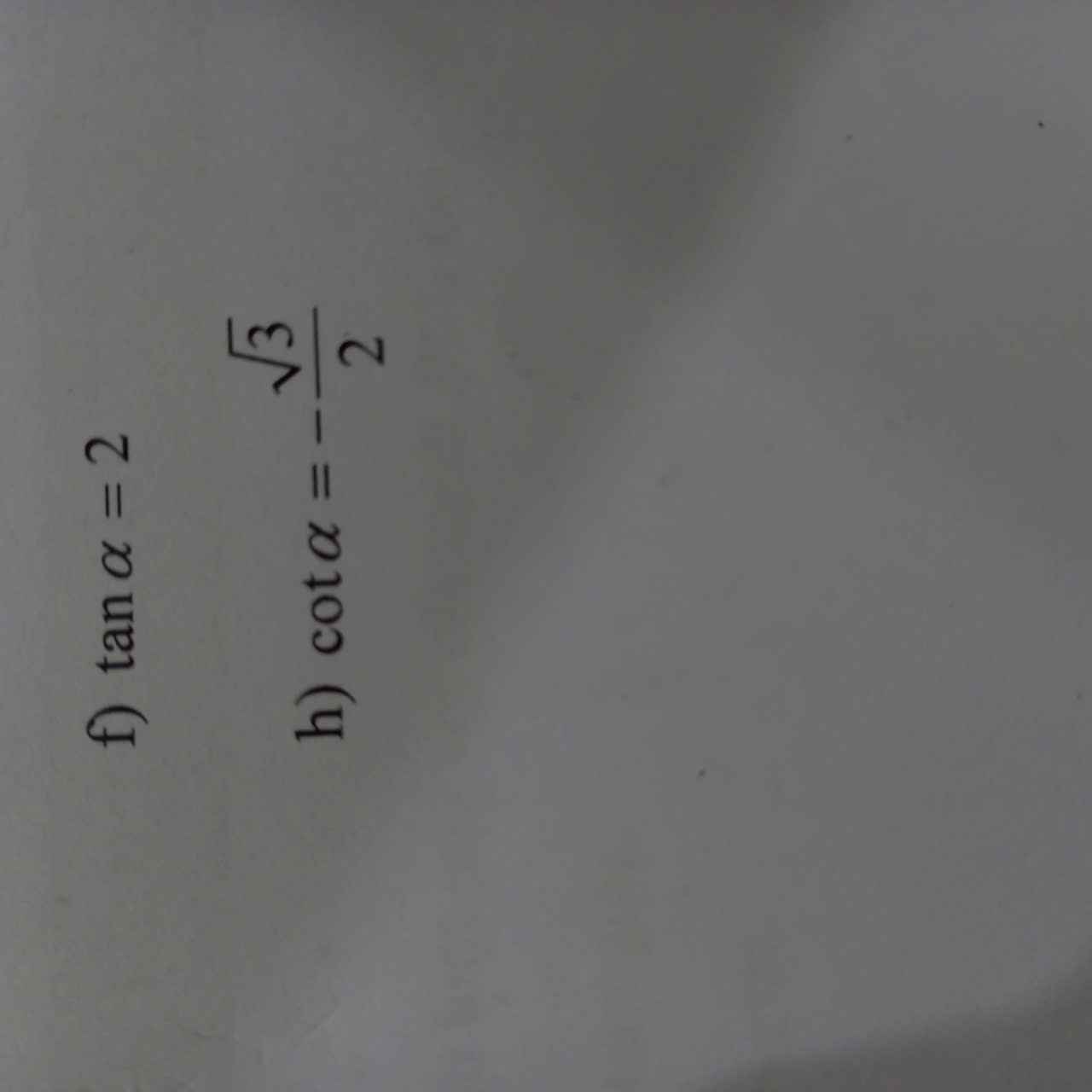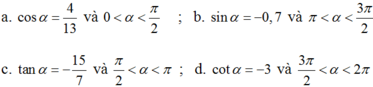Đề: Tính các giá trị lượng giác còn lại
`f) tan a = 1/(cota) = 2`
`=> cota = 1/2`
Lại có: `1 + tan^2 a = 1/(cos^2 a)`
`=> 1 + 2^2 = 1/(cos^2 a)`
`=> 5 = 1/(cos^2 a)`
`=> cos^2 a = 1/5`
`=> cos a = 1/sqrt{5} (`Vì `tana > 0)`
`=> sina = sqrt{1 - 1/5} = 2/sqrt{5} `
Vậy ...
`h) cota = -sqrt{3}/2`
`=> tana = 1/cota = -2/sqrt{3}`
Lại có: `1 + tan^2 a = 1/(cos^2 a)`
`=> 1 + 4/3 = 1/(cos^2 a)`
`=> 7/3 = 1/(cos^2 a)`
`=> cos^2 a = 3/7`
`=> cosa = -sqrt{3/7}` (Vì `cota < 0) `
`=> sina = sqrt{1 - 3/7} = 2/sqrt{7} `
Vậy ...
f.
\(cot\alpha=\dfrac{1}{tan\alpha}=\dfrac{1}{2}\)
\(1+tan^2\alpha=\dfrac{1}{cos^2\alpha}\Rightarrow cos^2\alpha=\dfrac{1}{1+tan^2\alpha}=\dfrac{1}{1+2^2}=\dfrac{1}{5}\)
\(\Rightarrow\left[{}\begin{matrix}cos\alpha=\dfrac{1}{\sqrt{5}}\Rightarrow sin\alpha=cos\alpha.tan\alpha=\dfrac{2}{\sqrt{5}}\\cos\alpha=-\dfrac{1}{\sqrt{5}}\Rightarrow sin\alpha=cos\alpha.tan\alpha=-\dfrac{2}{\sqrt{5}}\end{matrix}\right.\)
b.
\(tan\alpha=\dfrac{1}{cot\alpha}=-\dfrac{2}{\sqrt{3}}\)
\(cos^2\alpha=\dfrac{1}{1+tan^2\alpha}=\dfrac{1}{1+\left(-\dfrac{2}{\sqrt{3}}\right)^2}=\dfrac{3}{7}\)
\(\Rightarrow\left[{}\begin{matrix}cos\alpha=\sqrt{\dfrac{3}{7}}\Rightarrow sin\alpha=cos\alpha.tan\alpha=-\dfrac{2}{\sqrt{7}}\\cos\alpha=-\sqrt{\dfrac{3}{7}}\Rightarrow sin\alpha=\dfrac{2}{\sqrt{7}}\end{matrix}\right.\)
f)
Ta có:
\[
\tan a = \frac{\sin a}{\cos a} = 2
\]
Giả sử \(\sin a = 2k\) và \(\cos a = k\), khi đó:
\[
\tan a = \frac{\sin a}{\cos a} = \frac{2k}{k} = 2
\]
\[
\sin^2 a + \cos^2 a = 1
\]
Thay \(\sin a = 2k\) và \(\cos a = k\) vào ta có:
\[
(2k)^2 + k^2 = 1 \\
4k^2 + k^2 = 1 \\
5k^2 = 1 \\
k^2 = \frac{1}{5} \\
k = \frac{1}{\sqrt{5}}
\]
Vậy:
\[
\sin a = \frac{2}{\sqrt{5}}, \quad \cos a = \frac{1}{\sqrt{5}}
\]
Và:
\[
\sec a = \frac{1}{\cos a} = \sqrt{5}, \quad \csc a = \frac{1}{\sin a} = \frac{\sqrt{5}}{2}
\]
h)
Ta có:
\[
\cot a = \frac{\cos a}{\sin a} = \frac{\sqrt{3}}{2}
\]
Giả sử \(\cos a = \sqrt{3}k\) và \(\sin a = 2k\), khi đó:
\[
\cot a = \frac{\sqrt{3}k}{2k} = \frac{\sqrt{3}}{2}
\]
\[
\sin^2 a + \cos^2 a = 1
\]
Thay \(\cos a = \sqrt{3}k\) và \(\sin a = 2k\) vào ta có:
\[
(\sqrt{3}k)^2 + (2k)^2 = 1 \\
3k^2 + 4k^2 = 1 \\
7k^2 = 1 \\
k^2 = \frac{1}{7} \\
k = \frac{1}{\sqrt{7}}
\]
Vậy:
\[
\cos a = \frac{\sqrt{3}}{\sqrt{7}}, \quad \sin a = \frac{2}{\sqrt{7}}
\]
Và:
\[
\sec a = \frac{1}{\cos a} = \frac{\sqrt{7}}{\sqrt{3}}, \quad \csc a = \frac{1}{\sin a} = \frac{\sqrt{7}}{2}
\]