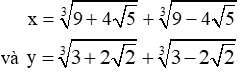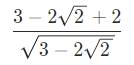\(\dfrac{3-2\sqrt{2}+2}{\sqrt{3-2\sqrt{2}}}=\dfrac{\left(\sqrt{2}-1\right)^2+2}{\sqrt{\left(\sqrt{2}-1\right)^2}}=\dfrac{\left(\sqrt{2}-1\right)^2+2}{\left|\sqrt{2}-1\right|}=\dfrac{\left(\sqrt{2}-1\right)^2+2}{\sqrt{2}-1}=\sqrt{2}-1+\dfrac{2}{\sqrt{2}-1}=\sqrt{2}-1+\dfrac{2\left(\sqrt{2}+1\right)}{\left(\sqrt{2}-1\right)\left(\sqrt{2}+1\right)}=\sqrt{2}-1+2\left(\sqrt{2}+1\right)=3\sqrt{2}+1\)
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho biểu thức với . a) Rút gọn biểu thức ; b) Tìm điều kiện của để ; c) Tìm các giá trị nguyên của để có giá trị nguyên; d)* Với , hãy tìm giá trị lớn nhất của . Bài 8: Cho biểu thức ; với . a) Tính giá trị biểu thức khi . b) Rút gọn biểu thức . c) So sánh với 1. d) Tìm để có giá trị nguyên.
cho biểu thức A = \(\dfrac{\sqrt{x}-1}{x-1}\)
a )Tính giá trị của biểu thức A tại x = -1
b ) Tính giá trị của biểu thức tại x = 1
Cho biểu thức B= x-2x/x -2 với x 0,x khác 4a, Rút gọn biểu thức Bb,Tính giá trị biểu thức B khi x=1c,Tính giá trị biểu thức B khi x=3+22d,Tìm x để B=1
Xem chi tiết
Cho biểu thức: P và Q (ĐKXĐ: )1. Tính giá trị của biểu thức P khi 2. Rút gọn biểu thức Q.Tìm các số hữu tỉ a để biểu thức M P.Q có giá trị nguyên
Đọc tiếp
Cho biểu thức: P =  và Q =
và Q =  (ĐKXĐ:
(ĐKXĐ: ![]() )
)
1. Tính giá trị của biểu thức P khi ![]()
2. Rút gọn biểu thức Q.
Tìm các số hữu tỉ a để biểu thức M = P.Q có giá trị nguyên
cho biểu thức: A=\(\dfrac{x^2+x-2}{x},B=\dfrac{x-1}{x+1}+\dfrac{3x-x^2}{x^2-1}\)
a)tính giá trị biểu thức với A=3
b)rút gọn biểu thức B
c)tìm giá trị của x để biểu thức P=A.B đạt giá trị nhỏ nhất
Không tính giá trị biểu thức, hãy sắp xếp giá trị của các biểu thức sau theo thứ tự tăng dần
\(A=2000^9\)
\(B=1996.1997.1998.1999.2000.2001.2002.2003.2004\)
\(C=1992.1994.1996.1998.2000.2002.2004.2006.2008\)
\(D=1980.1985.1990.1995.2000.2005.20010.2015.2020\)
Tính giá trị biểu thức:
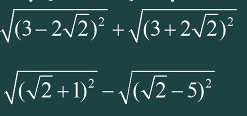
Tính giá trị biểu thức:
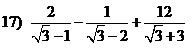
giúp mik nhanh vớiiiiii :(
cho biểu thức P.
P=\(\dfrac{\sqrt{x}}{\sqrt{x}-5}\) -\(\dfrac{10\sqrt{x}}{x-25}\)-\(\dfrac{5}{\sqrt{x}+5}\)
(x≥, x≠5)
a) rút gọn biểu thức P
b) tính giá trị P khi x=9
c) tính giá trị của x để biểu thức P=\(\dfrac{1}{2}\)
Tính giá trị biểu thức p với: