Các câu hỏi tương tự
Tính giá trị của biểu thức:
a) a sin 0 độ + b cos 0 độ + c sin 90 độ
b) a cos 90 độ + b sin 90 độ + c sin 180 độ
c) \(a^2sin90\) độ + b bình cos 90 độ + c bình cos 180 độ
1. Cho tam giác ABC có a \(=4\sqrt{2}\), c \(=10\), B\(=45^0\). Tính b, cos C, S, R, sin A, ha
Cho tam giác ABC. Chứng minh:
\(\frac{a^2-b^2}{\cos A+\cos B}+\frac{b^2-c^2}{\cos B+\cos C}+\frac{c^2-a^2}{\cos C+\cos A}=0\)
23 tháng 3 2022 lúc 9:39
cứuuuuuuu
\(a) A = a %2 sin 90 ^∘ + b ^2 cos 90 ^∘ + c ^2 cos 180 ^∘\)
\(b) B = 3 − sin ^2 90 ^∘ + 2 cos ^2 60 ^∘ − 3 tan ^2 45 ^∘\)
\(c) C = sin ^2 45 ^∘ − 2 sin ^2 50 ^∘ + 3 cos ^2 45 ^∘ − 2 sin ^2 40 ^∘ + 4 tan 55 ^∘ ⋅ tan 35 ^∘\)
22 tháng 10 2023 lúc 22:58
Cho cos x =2/3 và 0<x<90. Tính cos(90-x) và cot x
Cho sin a = 3/5 và cos a < 0 ; cos b = 3/4 và sin b > 0. Giá trị của sin(a - b) bằng :
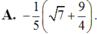
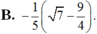
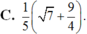
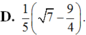
$\dfrac{\sin C}{\sin B}=2\cos A$
$\to \sin C=2\sin B\cos A$
$\to \sin C=\sin (A+B)-\sin (A-B)$
$\to \sin C=\sin(180^o-C)-\sin(A-B)$
$\to \sin C=\sin(C)-\sin(A-B)$
$\to \sin(A-B)=0$
$\to A-B=0$
$\to A=B$
$\to \Delta ABC$ cân tại $C$
Cho tam giác ABC và các mệnh đề : (III): cos(A + B - C) – cos 2C0 Mệnh đề đúng là : A. Chỉ (I). B. (II) và (III). C. (I) và (II). D. Chỉ (III).
Đọc tiếp
Cho tam giác ABC và các mệnh đề :
(III): cos(A + B - C) – cos 2C=0
Mệnh đề đúng là :
A. Chỉ (I).
B. (II) và (III).
C. (I) và (II).
D. Chỉ (III).
Tính giá trị các biểu thức sau:
a) A = a bình sin 90 độ + b bình cos 90 độ + c bình cos 180 độ
b) B = 3 - sin bình 90 độ + 2cos bình 60 độ - 3 tan bình phương 45 độ
c) C = sin bình phương 45 độ - 2 sin bình 50 độ +3 cos bình 45 độ - 2 sin bình 40 độ + 4 tan 55 độ. tan 35 độ
cho \(\dfrac{\pi}{2}\)<α<\(\pi\). tìm khẳng định đúng?
A. sin α<0 B. tan α>0 C. cot α>0 D. cos α<0
giải chi tiết nha