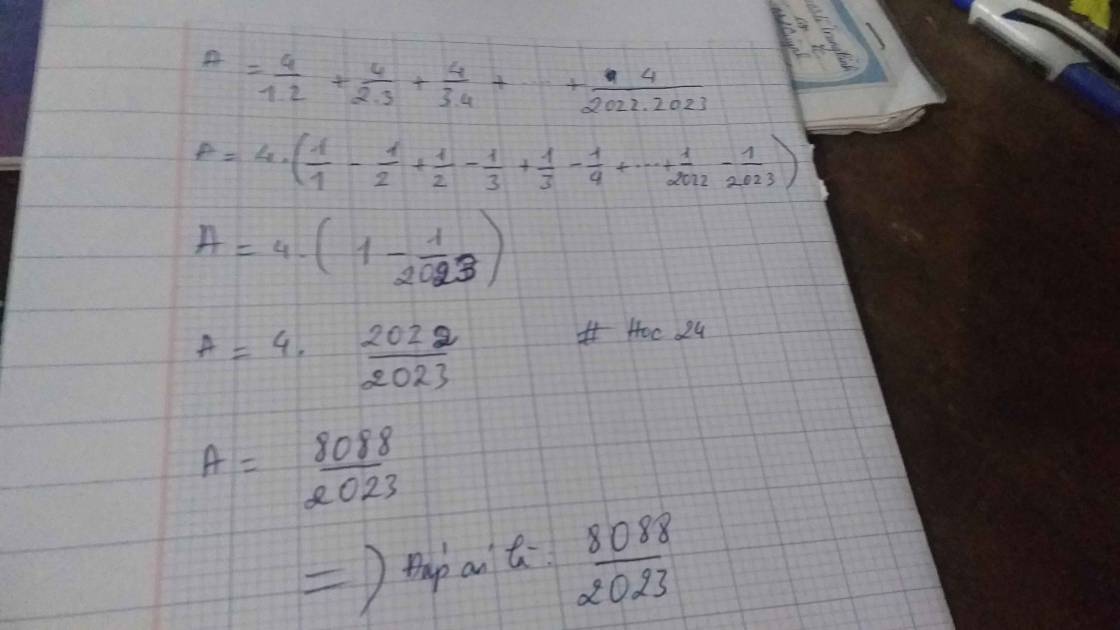\(A=\dfrac{4}{1\cdot2}+\dfrac{4}{2\cdot3}+\dfrac{4}{3\cdot4}+...+\dfrac{4}{2022\cdot2023}\\ A=4\cdot\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{2022\cdot2023}\right)\\ A=4\cdot\left(\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2022}-\dfrac{1}{2023}\right)\\ A=4\cdot\left(\dfrac{1}{1}-\dfrac{1}{2023}\right)\\ A=4\cdot\dfrac{2022}{2023}\\ A=\dfrac{8088}{2023}\)
giúp mình nhé! ngày mai mình kiểm tra đề cương r.
`A = 4/(1.2) + 4/(2.3) + ....+ 4/(2022.2023)`
`= 4 . (1/(1.2) + 1/(2.3) + ....+ 1/(2022.2023))`
`= 4 . (1 - 1/2 + 1/2 - 1/3 +.....+ 1/2022 - 1/2023)`
`= 4 . (1 - 1/2023)`
`= 4 . 2022/2023`
`= 8088/2023`