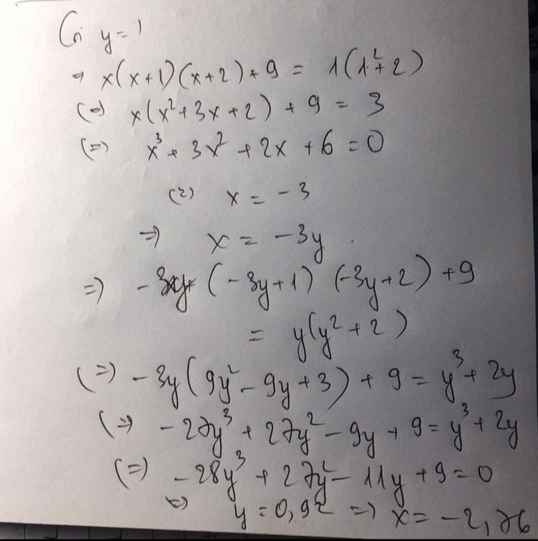Các câu hỏi tương tự
Cho x,y,z là các số thực dương thoả mãn \(x+y+z=xyz\) . Chứng minh rằng:
\(\frac{2}{\sqrt{1+x^2}}+\frac{1}{\sqrt{1+y^2}}+\frac{1}{\sqrt{1+z^2}}\le\frac{9}{4}\)
Cho x,y,z là các số thực dương thoả mãn \(x+y+z=xyz\) . Chứng minh rằng:
\(\frac{2}{\sqrt{1+x^2}}+\frac{1}{\sqrt{1+y^2}}+\frac{1}{\sqrt{1+z^2}}\le\frac{9}{4}\)
tìm các cặp số nguyên x,y thoả mãn x^2+xy=2022x+2023y+2024 (cần gấp)
bài 1: cho x,y thuộc R thoả mãn x^3+y^3+3.(x^2+y^2)+4.(x+y)+4=0 với xy>0
Tìm Max M = \(\frac{1}{x}+\frac{1}{y}\)
cac ban oi giup minh. minh dang can gap.
bài 1: tìm tất cả các cặp số nguyên (x,y) thoả mãn phương trình:
x^2-25=y.(y+6)
cac ban oi giup minh. minh dàng can gap
Cho: \(x;y;z\) là các số thực thoả mãn điều kiện: \(\frac{3}{2}x^2+y^2+z^2+yz=1\)
Tìm giá trị lớn nhất của: \(A=x+y+z\)
Giúp tôi
Cho x,y >0 thoả mãn x+y=1
Tìm min A= 1/x + 4/y
1:Tìm GTNN x^2+y^2 biết :(x^2-y^2+1)+4x^2y^2-x^2-y^2=0
2:Cho a nhỏ hơn hoặc =a,b,c nhỏ hơn hoặc =1.Tìm GTNN,GTLN của biểu thức:P=a+b+c-ab-bc-ca
3:cho các số thực nguyên thỏa mãn điều kiện :x^2+y^2+z^2 nhỏ hơn hoặc = 27.Tìm giá trị nhỏ nhất ,GTLN x+y+z+xy+yz+zx
4: cho x,y dương thỏa mãn dk: x+y=1.Tìm GTNN:M=(x+1/x)+(y+1/y)
17 tháng 2 2022 lúc 23:39
Mọi người giúp em bài này với ạ:
Cho các số thực dương x,y thỏa mãn x + y ≥ 3
Chứng minh rằng : \(x+y+\dfrac{1}{2x}+\dfrac{2}{y}\ge\dfrac{9}{2}\)