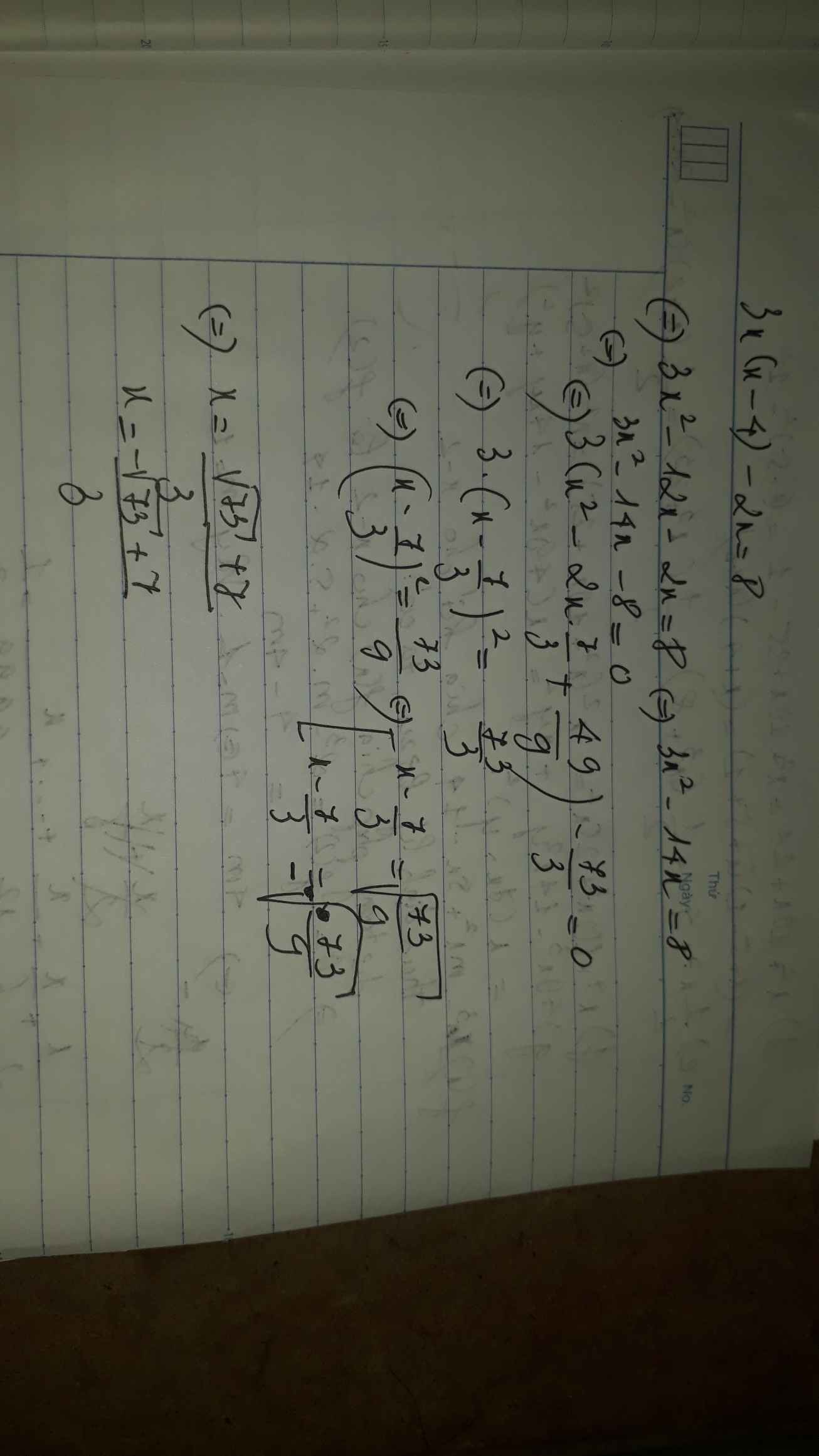Ta có: \(3x\left(x-4\right)-2x=8\)
\(\Leftrightarrow3x^2-12x-2x-8=0\)
\(\Leftrightarrow3x^2-14x-8=0\)
\(\text{Δ}=\left(-14\right)^2-4\cdot3\cdot\left(-8\right)=292\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{14-2\sqrt{73}}{6}=\dfrac{7-\sqrt{73}}{3}\\x_2=\dfrac{14+2\sqrt{73}}{6}=\dfrac{7+\sqrt{73}}{3}\end{matrix}\right.\)
3x ( x - 4 ) -2x = 8
3\(x^2\)-12x-2x = 8
3\(x^2\)-14x = 8
3\(x^2\) - 14x - 8 = 0
Khi ở dạng chuẩn, hãy tìm a, b và c của phương trình ban đầu và gán các giá trị đó vào công thức nghiệm của phương trình bậc hai.
a = 3
b = -14
c = -8
\(\dfrac{-\left(-14\right)_-+\sqrt{\left(-14\right)^2-4.3\left(-8\right)}}{2.3}\)
= \(\dfrac{14_-+\sqrt{73}}{2.3}\)