Đáp án C.
Ta có 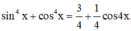 , khi đó phương trình đã cho trở thành:
, khi đó phương trình đã cho trở thành:
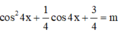
![]()
Đặt t = cos4x mà ![]() khi đó (*)
khi đó (*) ![]()
Xét hàm số ![]() trên [-1;0] có
trên [-1;0] có 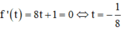
Tính 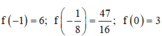
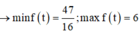
Để phương trình đa cho có 4 nghiệm thuộc 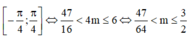
Đáp án C.
Ta có 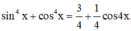 , khi đó phương trình đã cho trở thành:
, khi đó phương trình đã cho trở thành:
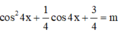
![]()
Đặt t = cos4x mà ![]() khi đó (*)
khi đó (*) ![]()
Xét hàm số ![]() trên [-1;0] có
trên [-1;0] có 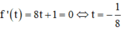
Tính 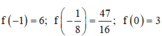
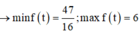
Để phương trình đa cho có 4 nghiệm thuộc 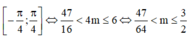
Gọi S là tổng tất cả các giá trị nguyên m < 64 để phương trình log 5 2 - x = log 5 x + m có nghiệm. Tìm S:
A. 2013
B. 2016
C. 2018
D. 2015
Gọi S là tập tất cả các giá trị nguyên của tham số m với m < 64 để phương trình log 1 5 x + m + log 5 2 - x = 0 có nghiệm. Tính tổng tất cả các phần tử của S
A. 2018
B. 2016
C. 2015
D. 2013
Tìm tất cả giá trị của tham số thực m để phương trình 8 sin 2 x - 10 sin x + 2 - m = log 2 2 sin x + m + 1 2 sin x - 1 2 có đúng bốn nghiệm phân biệt thuộc đoạn [ 0 ; 5 π 6 )
A. m ∈ - 17 8 ; - 2
B. m ∈ [ - 17 8 ; - 2 )
C. Không có giá trị của thỏa mãn.
D. m ∈ - 17 8 ; - 1
Tìm tất cả các giá trị của m để phương trình sin 4 x + cos 4 x + cos 2 4 x = m có bốn nghiệm phân biệt thuộc đoạn - π 4 ; π 4
A. m ≤ 47 64 h o ặ c m ≥ 3 2
B. 47 64 < m < 3 2
C. 47 64 < m ≤ 3 2
D. 47 64 ≤ m ≤ 3 2
Tìm tất cả các giá trị của tham số m để phương trình 1 3 cos 3 x − 3 cos 2 x + 5 cos x − 3 + 2 m = 0
có đúng bốn nghiệm phân biệt thuộc đoạn 0 ; 2 π .
A. − 3 2 < m < − 1 3
B. 1 3 ≤ m < 3 2
C. 1 3 < m < 3 2
D. − 3 2 ≤ m ≤ − 1 3
Tìm tất cả các giá trị của m để phương trình log 2 3 x − 2 − log 2 3 x + 1 = m có 3 nghiệm phân biệt?
A.m > 3
B. m < 2
C. m > 0
D. m=0
Tìm tất cả các giá trị của m để phương trình x 4 − 2 x 2 − m = 0 có bốn nghiệm phân biệt.
A. − 2 < m < 0
B. 0 < m < 1
C. − 1 < m < 2
D. − 1 < m < 0
Tìm tất cả các giá trị của m để phương trình sin 4 x + cos 4 x + cos 2 4 x = m có 4 nghiệm phân biệt thuộc đoạn - π 4 ; π 4 .
A. m ≤ 47 64 hoặc m ≥ 3 2
B. 47 64 < m < 3 2
C. 47 64 < m ≤ 3 2
D. 47 64 ≤ m ≤ 3 2
Cho phương trình 1 + cos x cos 4 x − m cos x = m sin 2 x . Tìm tất cả các giá trị của m để phương trình có đúng 3 nghiệm phân biệt thuộc 0 ; 2 π 3
A. m ∈ − 1 2 ; 1 2
B. m ∈ − ∞ ; − 1 ∪ 1 ; + ∞
C. m ∈ − 1 ; 1
D. m ∈ − 1 2 ; 1