Đáp án là B
Cách 1. Sử dụng công thức tính nhanh ta có
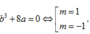
Cách 2. Nhận xét m thỏa mãn thì –m cũng thỏa mãn và hàm số có 3 điểm cực trị khi và chỉ khi m≠ 0 suy ra chọn B
Đáp án là B
Cách 1. Sử dụng công thức tính nhanh ta có
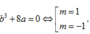
Cách 2. Nhận xét m thỏa mãn thì –m cũng thỏa mãn và hàm số có 3 điểm cực trị khi và chỉ khi m≠ 0 suy ra chọn B
Tìm tất cả các giá trị của tham số m để đồ thị hàm số: y = x 4 - 2 m 2 x 2 + 1 có ba điểm cực trị là ba đỉnh của một tam giác vuông cân.
A. m =1
B. m= ±1
C. m= -1
D. m≠0
Tìm tất cả các giá trị của tham số m để ba điểm cực trị của đồ thị hàm số y = x 4 + 2 m − 2 x 2 + 1 − m là ba đỉnh của một tam giác vuông
A. m = 0
B.
C. m = -1
D. m = 1
Tìm tất cả các giá trị của tham số m để ba điểm cực trị của đồ thị hàm số y = x 4 + 2 m - x x 2 + 1 - m là ba đỉnh của một tam giác vuông
A. m = -1
B. m = 1
C. m = 0 hoặc m = 1
D. = 0
Tìm giá trị thực của tham số m để ba điểm cực trị của đồ thị hàm số y = x 4 − 2 m + 1 x 2 − m + 1 là ba đỉnh của một tam giác vuông là
A. m = 0
B. m = 2
C. m = 1
D. m = -1
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = 2 x 4 - m x 2 + 1 có ba điểm cực trị lập thành một tam giác vuông.
A. m = - 2 5 3
B. m = 2 6 3
C. m = 0
D. m = 2 2 3
Cho hàm số y = x 3 - 3 m x 2 + 2 ( m 2 - 1 ) x - m 3 - m (m là tham số). Gọi A, B là hai điểm cực trị của đồ thị hàm số và I(2;-2). Tổng tất cả các giá trị của m để ba điểm I, A, B tạo thành tam giác nội tiếp đường tròn có bán kính bằng 5 là
A. 20 17
B. - 2 17
C. 4 17
D. 14 17
Số giá trị của tham số m để ba điểm cực trị của đồ thị hàm số y = x 4 + 6 m − 4 x 2 + 1 − m là ba đỉnh của một tam giác vuông là
A. m = − 2 3
B. m = − 1 3
C. m = 2 3
D. m = 1 3
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x 4 + 2 m − 3 x 2 − m − 1 có ba điểm cực trị tạo thành một tam giác đều.
A. m = 3 2 − 3 3
B. m = 3 2 + 3 3
C. m = − 3 2 − 3 3
D. m = − 3 2 + 3 3
Tìm tất cả giá trị thực của tham số m để đồ thị hàm số y = x 4 − 2 m x 2 + 2 m − 3 có ba điểm cực trị là ba đỉnh của tam giác cân.
A. m ≥ 0.
B. m > 0.
C. m ≠ 0 .
D. m < 0.