Các câu hỏi tương tự
Cho hình đa diện ABCDEF như sau:Biết rằng
∆
A
B
C
là tam giác đều cạnh a, (DEF) cân tại E; các cạnh AD, BE, CF vuông góc với mặt phẳng (DEF); tứ giác ADFC là hình chữ nhật;
A
D
C
F
3
2
a
,
B
E
a
.
Góc giữa mặt phẳng (ABC) và (DEF) có giá trị gần nhất với: A.
34
°
B....
Đọc tiếp
Cho hình đa diện ABCDEF như sau:
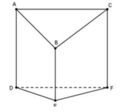
Biết rằng ∆ A B C là tam giác đều cạnh a, (DEF) cân tại E; các cạnh AD, BE, CF vuông góc với mặt phẳng (DEF); tứ giác ADFC là hình chữ nhật; A D = C F = 3 2 a , B E = a . Góc giữa mặt phẳng (ABC) và (DEF) có giá trị gần nhất với:
A. 34 °
B. 35 °
C. 36 °
D. 37 °
Cho tập hợp X gồm các số tự nhiên có 6 chữ số khác nhau có dạng
a
b
c
d
e
f
. Từ tập X lấy ngẫu nhiên một số. Tính xác suất để số lấy ra là số lẻ và thõa mãn
a
b
c
d
e
f
. A.
29
68040
B.
1
2430
C. ...
Đọc tiếp
Cho tập hợp X gồm các số tự nhiên có 6 chữ số khác nhau có dạng a b c d e f . Từ tập X lấy ngẫu nhiên một số. Tính xác suất để số lấy ra là số lẻ và thõa mãn a < b < c < d < e < f .
A. 29 68040
B. 1 2430
C. 31 68040
D. 33 68040
Cho tập hợp X gồm các số tự nhiên có sáu chữ số đôi một khác nhau có dạng
a
b
c
d
e
f
¯
. Từ tập hợp X lấy ngẫu nhiên một số. Xác xuất để số lấy ra là số lẻ và thỏa mãn
a
b
c
d
e
f
là A.
33
68040...
Đọc tiếp
Cho tập hợp X gồm các số tự nhiên có sáu chữ số đôi một khác nhau có dạng a b c d e f ¯ . Từ tập hợp X lấy ngẫu nhiên một số. Xác xuất để số lấy ra là số lẻ và thỏa mãn a < b < c < d < e < f là
A. 33 68040
B. 1 2430
C. 31 68040
D. 29 68040
Cho hình vuông ABCD. Dựng khối da diện ABCDEF , trong đó
E
F
2
a
và song song với AD (tham khảo hình vẽ bên). Tất cả các cạnh còn lại của khối đa diện ABCDEF bằng a. Tính thể tích V của khối đa diện ABCDEF. A.
V
2
a
3
6
. B.
V
5...
Đọc tiếp
Cho hình vuông ABCD. Dựng khối da diện ABCDEF , trong đó E F = 2 a và song song với AD (tham khảo hình vẽ bên). Tất cả các cạnh còn lại của khối đa diện ABCDEF bằng a. Tính thể tích V của khối đa diện ABCDEF.
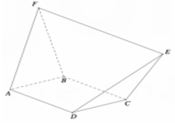
A. V = 2 a 3 6 .
B. V = 5 2 a 3 6 .
C. V = 2 a 3 3
D. V = 2 a 3 12
Cho hình vuông ABCD. Dựng khối da diện ABCDEF , trong đó EF2a và song song với AD (tham khảo hình vẽ bên). Tất cả các cạnh còn lại của khối đa diện ABCDEF bằng a. Tính thể tích V của khối đa diện ABCDEF. A. V
2
a
3
6
B. V
5
2
a
3
6...
Đọc tiếp
Cho hình vuông ABCD. Dựng khối da diện ABCDEF , trong đó EF=2a và song song với AD (tham khảo hình vẽ bên). Tất cả các cạnh còn lại của khối đa diện ABCDEF bằng a. Tính thể tích V của khối đa diện ABCDEF.
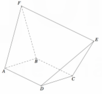
A. V = 2 a 3 6
B. V = 5 2 a 3 6
C. V = 2 a 3 3
D. V = 2 a 3 12
Số véc- tơ khác 0 → có điểm đầu, điểm cuối là hai trong 6 đỉnh của lục giác ABCDEF là
A. P 6
B. C 6 2
C. A 6 2
D. 36
Số véctơ khác
0
→
có điểm đầu và điểm cuối là hai trong 6 đỉnh của lục giác ABCDEF là A.
P
6
B. 36 C.
C
6
2
D.
A
6
2
Đọc tiếp
Số véctơ khác 0 → có điểm đầu và điểm cuối là hai trong 6 đỉnh của lục giác ABCDEF là
A. P 6
B. 36
C. C 6 2
D. A 6 2
Cho lục giác đều ABCDEF tâm O như hình bên. Tam giác EOD là ảnh của tam giác AOF qua phép quay tâm O góc quay
α
.
Tìm
α
.
A.
α
60
°
B.
α
−
60
°
C.
α
120
°
D.
α
−
120
°
Đọc tiếp
Cho lục giác đều ABCDEF tâm O như hình bên.
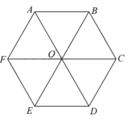
Tam giác EOD là ảnh của tam giác AOF qua phép quay tâm O góc quay α . Tìm α .
A. α = 60 °
B. α = − 60 °
C. α = 120 °
D. α = − 120 °
Cho lục giác đều ABCDEF tâm O như hình bên. Tam giác EOD là ảnh của tam giác AOF qua phép quay tâm O góc quay α . Tìm α.
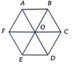
A. 30°
B. 60°
C. 90°
D. 120°


