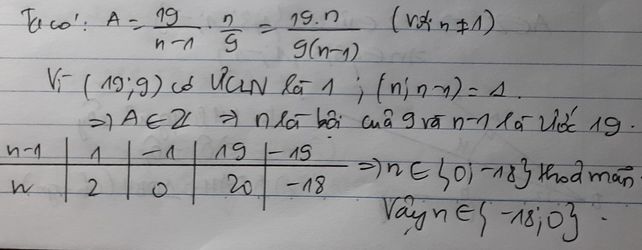Để tích 2 PS là số nguyên thì 19⋮n-1 và n⋮9
⇒n-1∈Ư(19),9∈B(n)
⇒Ư(19)={\(\pm\)1;\(\pm\)19}
⇒n-1=1 ⇒n-1=19
⇒n-1=-1 ⇒n-1=-19
⇒n∈{2;20;0;-18} nhưng 9∈B(n)
⇒n∈{0;-18}
Giải:
Ta gọi tích hai số là A
Ta có:
\(A=\dfrac{19}{n-1}.\dfrac{n}{9}=\dfrac{19.n}{\left(n-1\right).9}\) (với n ≠ 1)
Vì \(ƯCLN\left(19;9\right)=1\) \(;ƯCLN\left(n;n-1\right)=1\)
\(\Rightarrow A\in Z\)
\(\Rightarrow n\in B\left(9\right)\) và \(\left(n-1\right)\inƯ\left(19\right)\)
Ta có bảng giá trị:
| n-1 | 1 | -1 | 19 | -19 |
| n | 2 | 0 | 20 | -18 |
\(\Rightarrow n\in\left\{-18;0\right\}\) (t/m)
Vậy \(n\in\left\{-18;0\right\}\)