Chọn A
Đặt t = 4 - x 2 ⇒ x 2 = 4 - t 2 ⇒ x d x = - t d t
Khi đó ∫ x 3 4 - x 2 d x = ∫ ( 4 - t 2 ) ( - t d t ) t = ∫ ( t 2 - 4 ) d t = t 3 3 - 4 t + C = 4 - x 2 3 3 - 4 4 - x 2 + C = - 1 3 x 2 + 8 4 - x 2 + C
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho hàm số
F
(
x
)
a
x
3
+
b
x
2
+
c
x
+
1
là một nguyên hàm của hàm số f(x) thỏa mãn f(1) 2, f(2) 3, f(3) 4. Hàm số F(x) là
Đọc tiếp
Cho hàm số F ( x ) = a x 3 + b x 2 + c x + 1 là một nguyên hàm của hàm số f(x) thỏa mãn f(1) = 2, f(2) = 3, f(3) = 4. Hàm số F(x) là
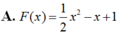
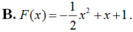
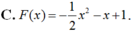
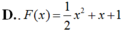
Cho hàm số f(x) liên tục trên khoảng (-2; 3). Gọi F(x) là một nguyên hàm của f(x) trên khoảng (-2; 3). Tính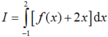 
, biết F(-1) = 1, F(2) = 4.
A. I = 6.
B. I = 10.
C. I = 3.
D. I = 9.
Tìm nguyên hàm F(x) của hàm số
f
(
x
)
3
+
cos
4
πx
4
,
F
(
4
)
2
Đọc tiếp
Tìm nguyên hàm F(x) của hàm số f ( x ) = 3 + cos 4 πx 4 , F ( 4 ) = 2
24 tháng 1 2022 lúc 22:03
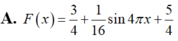
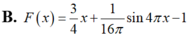
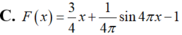
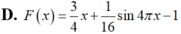
Cho hàm số \(f\left(x\right)\) có đạo hàm bằng \(f'\left(x\right)=x^2\left(x-1\right)^3\left(x-2\right)\) . Số điểm cực trị của hàm số \(f\left(x\right)\) bằng:
A.0 B.1 C.2 D.3
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:a) f(x)
(
25
-
x
2
)
trên đoạn [-4; 4]b) f(x) |
x
2
– 3x + 2| trên đoạn [-10; 10]c) f(x) 1/sinx trên đoạn [π/3; 5π/6]d) f(x) 2sinx + sin2x trên đoạn [0; 3π/2]
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) f(x) = ( 25 - x 2 ) trên đoạn [-4; 4]
b) f(x) = | x 2 – 3x + 2| trên đoạn [-10; 10]
c) f(x) = 1/sinx trên đoạn [π/3; 5π/6]
d) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
tính nguyên hàm của hàm số f(x)dfrac{2x+1}{x^4+2x^3+x^2}
Đọc tiếp
tính nguyên hàm của hàm số f(x)=\(\dfrac{2x+1}{x^4+2x^3+x^2}\)
Cho hàm số
y
f
(
x
)
có đạo hàm
f
(
x
)
(
x
+
1
)...
Đọc tiếp
Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = ( x + 1 ) ( x - 2 ) 2 ( x - 3 ) 3 ( x + 5 ) 4 . Hỏi hàm số y = f ( x ) có mấy điểm cực trị?
A. 2
B. 3
C. 4
D. 5
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$
Cho hàm số y f( x) có đạo hàm
f
(
x
)
(
x
+
1
)
4
(
x
-
2
)
5
(
x
+
3
)
3
Số điểm...
Đọc tiếp
Cho hàm số y= f( x) có đạo hàm f ' ( x ) = ( x + 1 ) 4 ( x - 2 ) 5 ( x + 3 ) 3 Số điểm cực trị của hàm số f x là
A. 5
B. 3
C. 1
D. 2
Cho hàm số f(x) có đạo hàm f ' ( x ) = x 2 ( x - 1 ) 3 ( x - 2 ) 4 ( x - 3 ) 5 , ∀ x ∈ ℝ . Số điểm cực trị của hàm số đã cho là
A. 1
B. 4
C. 2
D. 3