\(y'=2x-m=0\Rightarrow x=\dfrac{m}{2}\)
BBT:
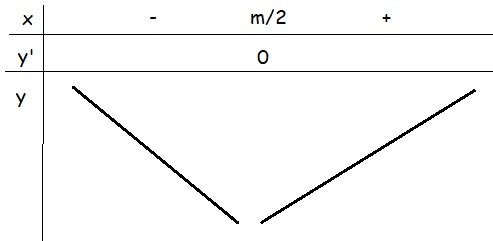
Từ BBT ta thấy hàm đồng biến trên \(\left(1;+\infty\right)\Rightarrow\left(1;+\infty\right)\subset\left(\dfrac{m}{2};+\infty\right)\)
\(\Rightarrow\dfrac{m}{2}\le1\)
\(\Rightarrow m\le2\)
cho hs y= x^3 + 3x^2 - mx - 4
tìm m để hàm số luôn đồng biến trên (âm vô cực, 0)
Tìm m để hàm số \(y=\dfrac{x^2-8x}{8x+8m}\)đồng biến trên \(\left(1;+\infty\right)\)
Tìm m để hàm số y = x 3 - x 2 + m x - 1 đồng biến trên (1,2)
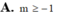
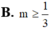
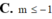
Tìm tất cả các giá trị thực của tham số m để hàm số y = x + m x + 1 đồng biến trên từng khoảng xác định của nó
A.
B. 
C.
D. 
định m để hàm số y=1/3x3 -2x2+mx-2 đồng biến trên tập xác định
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 3 x 2 + mx + 2 đồng biến trên R
A.m ≥ 3.
B. m > 3.
C. m < 3.
D. m ≤ 3.
tìm tất cả các giá trị thực của tham số m để hàm số y= x 3 - 3 x 2 - m x + 2 đồng biến trên R.
Trong tất cả các giá trị của tham số mm để hàm số y=\dfrac{1}{3} x^{3} +mx^{2} -mx-my=31x3+mx2−mx−m đồng biến trên \mathbb{R},R, giá trị nhỏ nhất của mm là
Tìm tập hợp tất cả các giá trị của tham số thực m để hàm số y = ln x 2 + 1 - m x + 1 đồng biến trên khoảng ( -∞; +∞).
A. ( - ∞ ; - 1 ]
B. ( - ∞ ; - 1 )
C. - 1 ; 1
D. Đáp án khác
![[柠檬]๛Čɦαŋɦ ČŠツ](https://hoc24.vn/images/avt/avt6342624_256by256.jpg)
