Lời giải:
BPT $\Leftrightarrow x>1-3m$
Để BPT có nghiệm với mọi $x\in [-1;3]$ thì $1-3m< -1$
$\Leftrightarrow m> \frac{2}{3}$
Lời giải:
BPT $\Leftrightarrow x>1-3m$
Để BPT có nghiệm với mọi $x\in [-1;3]$ thì $1-3m< -1$
$\Leftrightarrow m> \frac{2}{3}$
Tìm giá trị thực của tham số m để đường thẳng d: y=2x+m tiếp xúc với parabol P: y=m−1x2+2mx+3m−1.
A.m=−1.
B.m=0.
C.m=2.
D.m=1.
Tìm m để bpt m2x+ m( x+1) -2( x-1) > 0 nghiệm đúng với mọi x ∈ [-2,1]
A. 0 < m < 3/2
B. m > 0
C. m < 3/2
D. 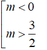
Bài 1. Tìm m để f (x)=mx^2 -2(m-1)x+4m-1 luôn dương Bài 2 tìm tất cả các giá trị của tham số m để bất phương trình sau có nghiệm đúng với mọi a.5x^2-x+m>0 b.m(m+2)x^2+2mx+2>0
Cho bpt: (m-2)x^2 + 2(4-3m)x + 10m -11 ≤ 0 (1). Gọi S là tập hợp các số nguyên dương m để bpt đúng với mọi ∀x < -4. Tìm số phần tử của S.
Tìm đk của m để bpt sau nghiệm đúng trên khoảng đã chỉ ra :
1. \(\left(m+1\right)x^2-2mx+4m\)> 0 với mọi x<0
2.\(_{x^2-2mx+3m-2>0}\)với x thuộc khoảng từ 1 đến 2
1. Tìm m để hệ bpt sau có nghiệm duy nhất:
\(\left\{{}\begin{matrix}x^2+2x+m+1\le0\\x^2-4x-6\left(m+1\right)< 0\end{matrix}\right.\)
2. Giải bpt sau
\(\dfrac{\left|x^2-x\right|-2}{x^2-x-1}\ge0\)
1/ Tìm các giá trị của tham số m để bpt ( m-1) x^2- ( m-1) x+1>0 nghiệm đúng vs mọi giá trị của x. 2/ Tìm giá trị của tham số m để pt x^2 - ( m-2) x+m^2 -4m=0 có 2 nghiệm trái dấu. 3/ Tìm giá trị của tham số m để pt x^2 -mx+1=0 có 2 nghiệm phân biệt.
Tìm m để bpt 2x2- (2m+1) x+ m2-2m+2≤ 0 nghiệm đúng với mọi x ∈ 1 2 ; 2
A. 2 ≤ m ≤ 21 + 2 34 10
B. m ≤ 21 + 2 34 10
C. m ≥ 2
D. 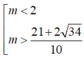
Tìm tất cả tham số `m` để bất phương trình `x^2-x+m(1-m)<=0` là hệ quả của bất phương trình `\sqrt{\sqrt{x-1}+4}-\sqrt{\sqrt{x-1}+1}>=1`?
`A.m=1/2`
`B.m<=0` hoặc `m>=1`
`C.m>=1`
`D.m<=0`