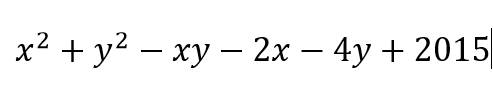Đặt \(A=x^2+y^2-xy-2x-4y+2015\)
\(=\frac14\left(4x^2+4y^2-4xy-8x-16y\right)+2015\)
\(=\frac14\left(4x^2-4xy+y^2+3y^2-8x-16y\right)+2015\)
\(=\frac14\left\lbrack\left(2x-y\right)^2-8x-4y+3y^2-12y\right\rbrack+2015\)
\(=\frac14\left\lbrack\left(2x-y\right)^2-4\left(2x-y\right)+4+3y^2-12y+12-16\right\rbrack+2015\)
\(=\frac14\left\lbrack\left(2x-y-2\right)^2+3\left(y-2\right)^2-16\right\rbrack+2015=\frac14\left(2x-y-2\right)^2+\frac34\left(y-2\right)^2-4+2015\)
\(=\frac14\left(2x-y-2\right)^2+\frac34\left(y-2\right)^2+2011\ge2011\forall x,y\)
Dấu '=' xảy ra khi \(\begin{cases}y-2=0\\ 2x-y-2=0\end{cases}\Rightarrow\begin{cases}y=2\\ 2x=y+2=2+2=4\end{cases}\Rightarrow\begin{cases}y=2\\ x=2\end{cases}\)