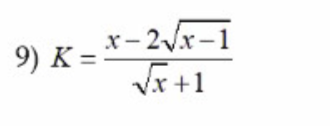Question

Tìm GTNN bằng cách đánh giá từng phần

giúp mình vơi mình cần gấp ạ

 

Answer 1

Lời giải:
$K=\frac{x-2\sqrt{x-1}}{\sqrt{x}+1}=\frac{(x-1)-2\sqrt{x-1}+1}{\sqrt{x}+1}$
$=\frac{(\sqrt{x-1}-1)^2}{\sqrt{x}+1}$
Ta thấy:

$(\sqrt{x-1}-1)^2\geq 0$ với mọi $x\geq 0$

$\sqrt{x}+1>0$ 

$\Rightarrow K\geq 0$

Vậy $K_{\min}=0$. Giá trị này đạt tại $\sqrt{x-1}-1=0$

$\Leftrightarrow x=2$